To enliven our discussion of arc length problems, I often challenge the
students in my calculus course to an arc length contest. Each student (or
team of students) is asked to find three examples of a continuous function f that satisfies
f(x) ≥ 0 on the interval 0 ≤ x ≤ 1;
f(0) = 0, f(1) = 0;
the area bounded by the graph of f and the x-axis between x=0
and x=1 is equal to 1.
The student must compute the arc length for each of her three
functions, and the winner of the contest is the one who has the function
with the smallest arc length on the unit interval. This is an interesting
open-ended problem for most students since they do not have much experience
in constructing functions that satisfy required conditions. I am often
surprised by some of the ingenuity students use in coming up with their
contest entries. The contest requires evaluation of two different integrals
for each function, one for the area and one for the arc length. Moreover, it is important for the students to recognize
when one of their functions gives rise to an improper integral for the arc
length since such an integral may be difficult to approximate accurately.
Thus the contest provides an opportunity to combine several topics from the
typical calculus syllabus.
The shortest curve enclosing an area of 1 square unit is a circle of radius . Its arc length is . Since a unit area is bounded by any curve in our contest toether with the interval [0,1], the length of a contest curve
cannot be less than . If
one imagines an ideal inextensible string of length L>1 nailed down at the
points (0,0) and (1,0), and pushed outward by a uniform pressure, then
the equilibrium curve (where the force due to the pressure is balanced by
the tension in the string in each small arc) has constant curvature in any
portion where it is smooth, so it is a circular arc. This suggests that an arc
of a circle joining the points (0,0) and (1,0) will yield the smallest
arc length for a curve satisfying the three conditions, as illustrated in
figure 1.
Figure 1
To achieve the area of 1, we would need
which yields a center for the circle at (0.5,0.35487517) with a
radius of r=0.6131365 and an arc length of 2.6831. This arc, whose length
is within 0.14 of being best possible, satisfies the three requirements, but
unfortunately is not the graph of a function and thus would violate the
rules of the contest.
Imagine now a situation where we have vertical walls at x=0 and x=1, a
floor at y=0, and a "rubber band" stretched between (0,0) and (1,0).
Inject a unit volume of fluid under the rubber band. The
region will fill to a semicircle and then extend upwards, keeping a
semicircular cap. Without the vertical walls we would just get the circular
bubble of Figure 1. The semicircle of radius 1/2 has area π/8. An
enclosed area of 1 could thus be obtained by extending the semicircle
upwards by a height of 1–π/8, in essence placing the semicircle atop a
rectangle with base along the unit interval. The two side walls of the
rectangle and the arc of the semicircle would then have a total length of 2+π/4 = 2.7853981634. Unfortunately, this is not the graph of a function,
either! However, we can get arbitrarily close to this length with a
continuous, piecewise-defined function by leaning the vertical walls in by
an amount ε and using a semicircle of radius 1/2–ε. This suggests that 2+π/4 is the greatest lower bound of the lengths of admissible curves.
The piecewise function just described has yet to be entered in the contest by any of
my students, however. The entries have always consisted of combinations of
the typical functions encountered in calculus: polynomials, radicals,
trigonometric functions, and logarithms. There are two observations that
greatly aid in constructing functions for the contest. First, students
quickly realize after an appropriate suggestion from the instructor that any
continuous function g that satisfies conditions (1) and (2) can be
modified to obtain a function f satisfying all three conditions by
dividing g by the value of its definite integral from x=0 to x=1.
Less obvious, however, is the fact that the best functions to
consider are those that are symmetric about the line x=1/2. Indeed, if the
function f satisfies conditions (1)-(3) and we define
,
then g will also satisfy conditions (1)-(3),
will be symmetric about the line x=1/2, and will have a smaller arc length
on [0,1] than f. To see why this holds, observe that the graph of
is concave up over the real line. Therefore the line segment
between any two points on the graph lies above the graph, which means that
for any a and b. If f is differentiable on [0,1], apply this
inequality with
and
for each x in
[0,1] and integrate over the interval to conclude that
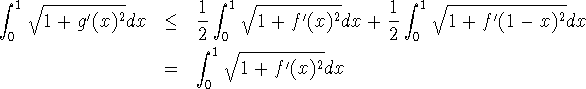
If f is only differentiable on the open interval (0,1), but the
improper arc length integral for f converges, then the inequality is still
valid by considering limits. The typical functions entered in the contest are differentiable
on at least the open unit interval.
The most familiar family of functions for many students are polynomials. The
only quadratic polynomial eligible for the contest is f(x)=6x(1–x), which
has an arc length of 3.24903. Many students will also investigate cubic
polynomials, but by our second observation above, this is a losing
proposition since if f is any cubic polynomial satisfying the contest
conditions, then
.
Therefore no eligible cubic polynomial has an arc length less than 3.24903.
There is hope for a fourth degree polynomial, however. Let
.
Conditions (2) and (3) yield two linear
equations for the four coefficients A,B, C, and D that can be reduced
to
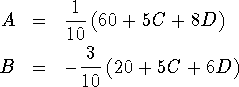
By our observation we will assume that f is
symmetric about the line x=1/2. Then
for all x in the unit interval. Therefore C= 2D. We know that f has roots at x=0 and x=1. The other potential roots would be at
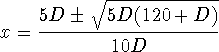
To satisfy condition (1) of the contest, these two roots
must be complex or, if real, must lie outside the open unit interval or be a double root at x = 1/2 (which occurs when D = −120). Investigating these possibilities reveals that condition (1) holds
when −120 ≤ D ≤ 30. Now the arc length of the polynomial f will be a function of the coefficient D. Figure 2 shows a graph of
this arc length function for −120 ≤ D ≤ 30.
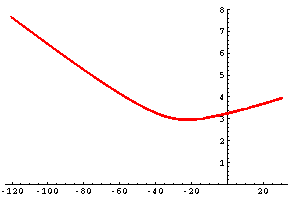
Figure 2
We see there is a minimum
which Mathematica determines to be 2.95752 at D= −22.4935. Therefore the
best 4th degree polynomial for the contest is
with an arc length of
2.95752.
One could continue to investigate higher degree polynomials to find
functions with arc length even less than 2.95752. For example, the 6th
degree polynomial
satisfies the conditions of the contest and has an arc length of 2.8796.
Such investigations become increasingly more difficult, however, because the
arc lengths become functions of more than one coefficient after invoking
requirements (2) and (3) and the symmetry assumption to find linear
relationships among the coefficients.
Besides polynomials, the other most popular functions the students use in
the contest are those that start with the sine function and a semicircle.
After adjusting for condition (3), these two choices lead to the entries
with an arc length of 3.3655, and
,
the upper half of an ellipse with an arc
length of 2.91946. [Note: The original version of this paper reported the arc length of the semi-ellipse as 2.91902.] The semi-ellipse has always won the contest, but just
barely. This year one group of students decided to investigate functions of
the form
for n > 0. Their three entries
consisted of the functions with n=1/100, n=1/2, and n=1. Based on
their numerical approximations, they conjectured that the arc length could
be made smaller by taking n closer to 0. Unfortunately, they failed to
realize the numerical difficulties in evaluating the improper integral for n=1/100 (with An = 1.013095. Derive, the computer algebra system we use
in class, gives a "dubious accuracy" warning and a value of 1.97361 for
the arc length using the default precision! However, the graph of this
function is concave down as suggested by Figure 3, a behavior that can be confirmed by computing the second derivative.
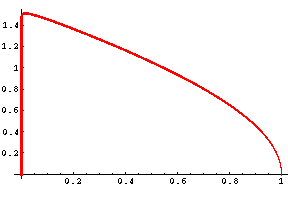
Figure 3
The graph has a maximum at approximately (0.015, 1.51). The
actual arc length will therefore be greater than the sum of the lengths of
the line segment connecting the origin with this maximum point and the
segment connecting the maximum point with (1,0). This sum is 3.313. The
arc length for n=1/2, with An = 1.716209468, is 2.91913 which just
barely beats out the semi-ellipse.
Could this group of students have done better? Using Mathematica to integrate xn arccos(x) on the interval [0,1] reveals that we should take
to have the function f(x) = Anxn arccos(x) satisfy condition (3) of the contest. After substituting this expression,
the arc length of f over the unit interval becomes
a function of n.
Figure 4
Figure 4 shows that this function has a minimum which
Mathematica computes to occur at n= 0.379358, yielding an arc length of 2.90467.
The function we just found is not symmetric, however. If we let
we obtain a function that is symmetric and has arc length 2.87535.
This is within 3.23% of the greatest lower bound of the lengths of admissible curves. The best
solution that I have found, though, that is built from the standard
functions of calculus is
with an arc length of 2.78946. The reason this works so well is that the
small exponent makes the sides of the graph very steep near x=0 and x=1
so that the graph approximates quite closely the semicircle sitting atop the
rectangle of height 1- π/8
as shown in Figure 5. Anyone have a better
entry for the contest?
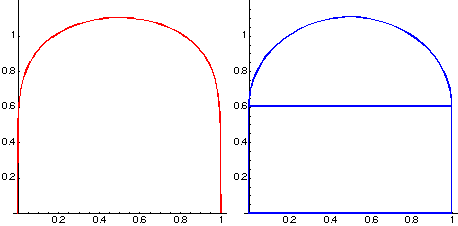
Figure 5
Students interested in the arc length contest might also be interested
in reading about the history of similar types of problems. Dido's
problem involves finding the figure with the greatest area among all
the plane figures bounded by a line and a curve of given length. The
arc length contest, posed in an equivalent minimization form, requires
that the curve be the graph of a function and that the figure by bounded
by the unit interval on the x-axis. Finding the closed plane
curve of given length enclosing the maximum area is the classic
isoperimetric problem. The isoperimetric problem, however, places no
restrictions on the shape of the figures involved. These, and more
general types of problems, can be studied with the calculus of variations.
Acknowledgment: I would like to thank Kurt Foster and the other
contributors to the usenet newsgroup, sci.math, for their suggestions and
comments about the arc length contest.
. Its arc length is 
. Since a unit area is bounded by any curve in our contest toether with the interval [0,1], the length of a contest curve
cannot be less than 
. If
one imagines an ideal inextensible string of length L>1 nailed down at the
points (0,0) and (1,0), and pushed outward by a uniform pressure, then
the equilibrium curve (where the force due to the pressure is balanced by
the tension in the string in each small arc) has constant curvature in any
portion where it is smooth, so it is a circular arc. This suggests that an arc
of a circle joining the points (0,0) and (1,0) will yield the smallest
arc length for a curve satisfying the three conditions, as illustrated in
figure 1.
,
and 
.
.
,
