


Construction
Animation
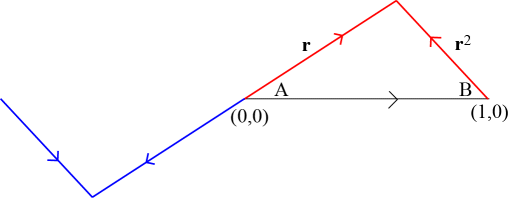
Recall that \({\bf{r}} = \left( \dfrac{1}{\phi}\right)^{\frac{1}{\phi}} = 0.74274\) where \(\phi\) is the golden ratio, and that A = 32.893818° and B = 46.98598225°. Now continue to repeat the construction on each of the four new segments to get the Z2 Golden dragon.
|
\({h_1}({\bf{x}}) = {g_1}{f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{0.623653} & { - 0.403372} \\
{0.403372} & {0.623653} \\
\end{array}} \right]{\bf{x}}\) |
scale by r, rotate by 32.894° |
|
\({h_2}({\bf{x}}) ={g_2}{f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{-0.623653} & { 0.403372} \\
{-0.403372} & {-0.623653} \\
\end{array}} \right]{\bf{x}}\) |
scale by r, rotate by −147.106° |
|
\({h_3}({\bf{x}}) ={g_1}{f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ - 0.376347} & { - 0.403372} \\
{0.403372} & { - 0.376347} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
1 \\
0 \\
\end{array}} \right]\) |
scale by r2, rotate by 133.014° |
|
\({h_4}({\bf{x}}) = {g_2}{f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 0.376347} & { 0.403372} \\
{-0.403372} & { 0.376347} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
-1 \\
0 \\
\end{array}} \right]\) |
scale by r2, rotate by −46.986° |
If H is the unique attractor for this IFS, then
\[H = h_1(H) \cup h_2(H) \cup h_3(H) \cup h_4(H) \]Rotating H by 180° counterclockwise is the same as applying the function g2 from the cyclic group Z2 to the set H. Because g2g2 = g1 (identity) and g2g1 = g2, we get
\[\begin{align} {g_2}(H) &= {g_2}\left( {{h_1}(H) \cup {h_2}(H) \cup {h_3}(H) \cup {h_4}(H)} \right)\\ \\ &= {g_2}{g_1}{f_1}(H) \cup {g_2}{g_2}{f_1}(H) \cup {g_2}{g_1}{f_2}(H) \cup {g_2}{g_2}{f_2}(H)\\ \\ &= {g_2}{f_1}(H) \cup {g_1}{f_1}(H) \cup {g_2}{f_2}(H) \cup {g_1}{f_2}(H)\\ \\ &= h_2(H) \cup h_1(H) \cup h_4(H) \cup h_3(H) = H \end{align}\]This shows that H has 180° rotational symmetry. Also notice that h1(H) = h2(H). That is because h2 does the same scaling to H as h1 but the two rotations differ by exactly 180°. Because of the 180° rotational symmetry of H, however, the result will be the same in both cases. You can see what happens by clicking on each of the buttons to the left to cover H with the four scaled and rotated copies.