Heighway Dragon Components

Ngai and Nguyen [2003] showed that the Heighway dragon is a countable union of closed geometrically similar disk-like planar sets, any two of which intersect at no more than one cut point. The following figure shows the largest (principle) component of the dragon in red.

The red component consists of one copy of the principle component scaled by 1/2 and rotated by 180°, two copies of the principle component scaled by 1/4, and four copies of the dragon scaled by 1/4, with two of them rotated by 180°. The four copies of the dragon form two copies of a twindragon.

You can add the pieces to the principle component by clicking on the buttons to the left in sequence.

The cut points for the principle component are at (1/3, 1/3) and (2/3, 0). These are the points where this component touches the smaller components are either side. The following image shows the cut points for some of the other components as they spiral towards either (0,0) on the left or (1,0) on the right.

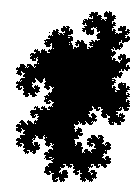
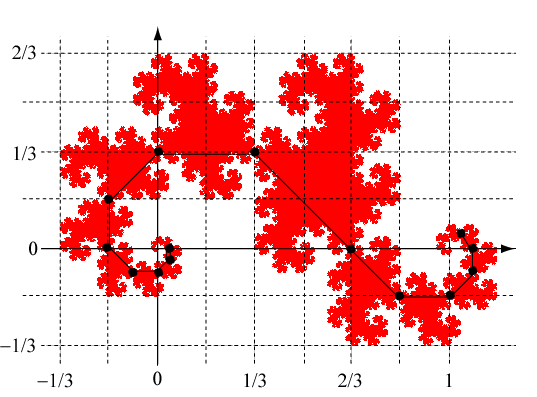
The cut points for the components to the left of the principle component are located at

\[\begin{array}{l} x = \frac{1}{3} \cdot \frac{1}{{{{\sqrt 2 }^{(n - 1)}}}} \cdot \sin \left( {(n + 3) \cdot {{45}^ \circ }} \right) \\ y = - \frac{1}{3} \cdot \frac{1}{{{{\sqrt 2 }^{(n - 1)}}}} \cdot \cos \left( {(n + 3) \cdot {{45}^ \circ }} \right) \\ \end{array}\]

for n ≥ 0. For the points in the figure, these are (1/3, 1/3), (0, 1/3), (-1/6, 1/6), (-1/6, 0), (-1/12, -1/12), (0, -1/12), (1/24, -1/24), and (1/24, 0).

The cut points for the components to the right of the principle component are located at

\[\begin{array}{l} x = 1 + \frac{1}{3} \cdot \frac{1}{{{{\sqrt 2 }^{(n - 1)}}}} \cdot \sin \left( {(n - 3) \cdot {{45}^ \circ }} \right) \\ y = - \frac{1}{3} \cdot \frac{1}{{{{\sqrt 2 }^{(n - 1)}}}} \cdot \cos \left( {(n - 3) \cdot {{45}^ \circ }} \right) \\ \end{array}\]

for n ≥ 1. For the points in the figure, these are (2/3, 0), (5/6, -1/6), (1, -1/6), (13/12, -1/12), (13/12, 0), and (25/24, 1/24).

You can get a sense of why these cut points arise and where by looking at the 10th iteration of the Heighway dragon starting with the unit line segment from (0,0) to (1,0). In the figure below, where the iteration is superimposed on top of the dragon, the places where the segments do not enclose a complete square are the locations where the cut points will arise in the limit as the number of iterations goes to infinity.

[Enlarge]

The figures above and the formulas for the cut points suggest that starting with the principle component, the other components can be obtained by scaling each component by \(1/\sqrt 2\) and rotating by 45° to get the next component in the spiral towards either (0,0) or (1,0). This is what actually happens. The one exception is that starting with the principle component, the first component to the right is scaled by 1/2 and not rotated (this can be seen in the figure showing the cut points). Otherwise, it is the same as the second component to the left. The rest of the components on the right are then scaled successively by \(1/\sqrt 2\) and rotated by 45°.

The figures below show how the components continue to repeat as you zoom in (going from left to right, as indicated by the square boxes). Click on each image for a larger view.

Let C₀ represent the principle component and let A be the area of this component. Label the components to the left as C_k for k from 1 to infinity. Because C_k is obtained from C₀ by a scaling by \(\left( 1/ \sqrt 2 \right)^k\), the area of C_k is equal to \({\left( {1/2} \right)^k}A\). Each component to the right of the principle component has the same area as the corresponding component to the left starting with k = 2. The total area, H, of the Heighway dragon is therefore \[H = A + \frac{1}{2}A + 2\left( {\frac{1}{4}A + \frac{1}{8}A + \ldots } \right) = A + \frac{1}{2}A + A = \frac{5}{2}A\]

Hence A = (2/5)H. The areas of the other components can be found by dividing by an appropriate power of 2.

We know that the principle component of the Heighway dragon consists of 4 copies of the dragon, each scaled by 1/4, by one copy of the principal component scaled by 1/2, and by two copies scaled by 1/4. Looking at the areas of these 7 pieces shows that

\[4\left( {\frac{1}{{16}}H} \right) + \frac{1}{4}A + 2\left( {\frac{1}{{16}}} \right)A = 4\left( {\frac{5}{{32}}A} \right) + \frac{1}{4}A + \frac{1}{8}A = \frac{5}{8}A + \frac{1}{4}A + \frac{1}{8}A = A\]

Therefore the seven parts of the principle component must be essentially disjoint.

 

1. Angle Chang and Tianrong Zhang. "The Fractal Geometry of the Boundary of Dragon Curves," J. Recreational Mathematics, Vol. 30, No. 1 (1999-2000), 9-22. [Available at http://poignance.coiraweb.com/math/Fractals/Dragon/Bound.html]
2. Sze-Man Ngai and Nhu Nguyen. "The Heighway Dragon Revisited," Discrete and Computational Geometry, Vol. 29, no. 4 (2003), 603-623. [Available at Springer Link or Professor Ngai's research website at Georgia Southern University].