


The iteration of the L-system generates the "dragon curve". The individual line segments never cross. Now take the nth iterate in the construction and draw a square lattice on the plane of size \({(\frac{1}{{\sqrt 2 }})^n}\), where n is even (if you want to do this with any n, it would be necessary to rotate the lattice by 45° and scale the grid by \({(\frac{1}{{\sqrt 2 }})}\)). Starting with an initial line of length 1, we can draw the segments in the dragon construction so that the corners always occur at these lattice points in the plane. Harter was the first to show that copies of the dragon could be fitted together to cover all lattice points. For example, shown below is the 6th iterate (in red) and three copies, each rotated by a multiple of 90°. The dot indicates the beginning of the curve (the tail). The lattice is of grid size 1/8.
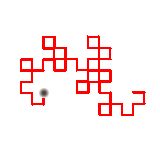

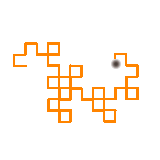

Geogebra
Animation
Now join each of the curves tail to tail by clicking on the buttons to the left in sequence.
The image below shows four copies of the 8th iterate of the Heighway dragon. Click on the play button to see an animation of the iterates starting at the beginning of each curve that demonstrates how each of the four different dragons fit together to tile the plane. The three buttons labeled slower, normal, and faster will adjust the drawing speed.
Higher order iterates would continue to cover lattice points on a smaller scale [Example with 10 iterations (pdf)]. In the limit, four copies of the dragon would exactly nestle together as you can demonstrate by clicking on the following buttons in sequence.

The four pieces form an image with 90° rotational symmetry. The entire plane can be covered by copies of this combined image [Example]. The plane can, in fact, be tiled by copies of the Heighway dragon in many ways. More details can be found in the paper by Davis and Knuth.
See the four rotated copies of the Heighway dragon done in counted cross-stitch.