The twindragon is constructed by placing two Heighway dragons side by side with the tail of one corresponding to the head of the other. One way to visualize the construction is to start with a horizontal line segment and replace this with two line segments above and two line segments below, each scaled by
r = \(1/ \sqrt 2\), such that the four line segments form a square. Now replace each of these four segments with two new segments at right angles and scaled by
r, alternating between placing the segments to the left and then to the right as you go around the square in the clockwise direction. Continue this construction, always alternating the new segments between left and right as you trace along the segments of the previous iteration starting at the original endpoint of the initial segment.. The following figure shows the first three iterations for this construction. In essence, the red segments are building one copy of the Heighway dragon going from left to right and the blue segments are building a second copy going from right to left as can be seen in the construction animation.

For an alternative view of how two Heighway dragons fit together to form the twindragon, see this animated demonstration.
Here is one way to visualize an IFS for the twindragon.
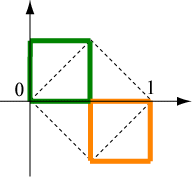
The dotted square is the initial set. Both the green and orange squares are obtained from the dotted square by scaling by \(1/ \sqrt 2\) and rotating by 45°. The orange square must then be translated so that the bottom left corner is moved to the point (1/2, −1/2). This yields the following IFS.
\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{1/2} & { - 1/2} \\
{1/2} & {1/2} \\
\end{array}} \right]{\bf{x}}\)
|
scale by \(1/ \sqrt 2\), rotate by 45°
|
\({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 1/2} & { - 1/2} \\
{1/2} & { 1/2} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
1/2 \\
-1/2 \\
\end{array}} \right]\)
|
scale by \(1/ \sqrt 2\), rotate by 45°
|
The twindragon consists of two self-similar pieces corresponding to the two functions in the IFS.

[Enlarge]
This is essentially the same L-system as for the Heighway dragon except with the axiom consisting of a segment that is drawn twice, but in opposite directions.
Angle 45
Axiom FX−−−−FX
F —> Z
X —> +FX−−FY+
Y —> −FX++FY−

The twindragon is self-similar with 2 non-overlapping copies of itself, each scaled by the factor
r < 1. Therefore the similarity dimension,
d, of the
attractor of the IFS is the solution to
\[\sum\limits_{k = 1}^2 {{r^d}} = 1 \quad \Rightarrow \quad d = \frac{{\log (1/2)}}{{\log (1/\sqrt 2 )}} = 2\]
Since the twindragon consists of two copies of the Heighway dragon, it has area 1. A twindragon starting with a segment of length b has area b2.
The boundary of the twindragon has the same dimension 1.523627 as the boundary of the Heighway dragon [
Details]. Because of the self-similarity of the twindragon, repeated applications of the IFS to the image of the boundary of the twindragon will produce scaled (and rotated) versions that fill in the twindragon as shown in the animation.






