


Recall that the twindragon consists of two copies of the Heighway dragon drawn side by side with the tail of one corresponding to the head of the other. The boundary of the twindragon is the union of 4 self-similar pieces. The first two are part of the boundary from one Heighway dragon and the last two are part of the boundary from the other Heighway dragon.


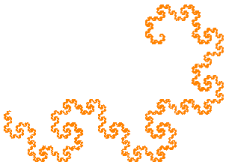

Put them together by clicking on the buttons to the left in sequence

To construct the boundary, start with the dashed figure (Level 0) in the following image, then replace each pair of segments with the four patterns shown to get Level 1.
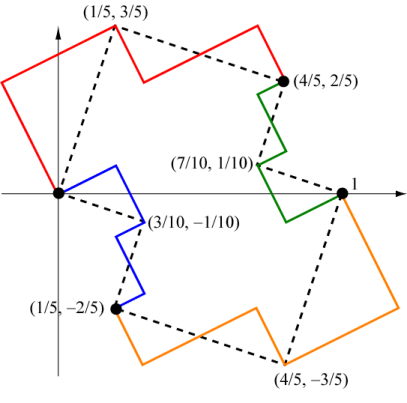
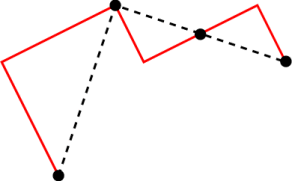
Notice that all four motifs are the same except for scale and how they are rotated. In addition, each motif consists of 3 self-similar parts. For example, the red motif consists of the following three parts.
Now iterate this construction by replacing each of those three parts by copies of that color's motif. Here is Level 2. The dotted line is Level 1.
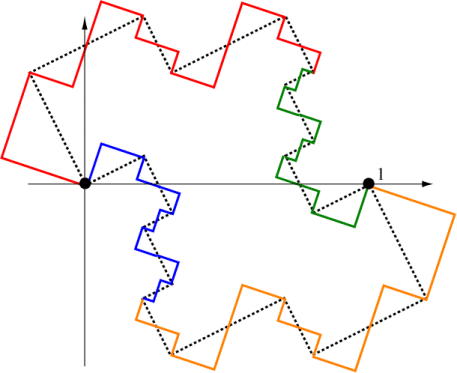
Repeat ad infinitum to construct the entire boundary around the twindragon.
Red Boundary:
|
\({R_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{1/2} & { - 1/2} \\
{1/2} & {1/2} \\
\end{array}} \right]{\bf{x}} \) |
scale by \(\frac{1}{\sqrt 2}\), rotate by 45° |
|
\({R_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ - 1/4} & { - 1/4} \\
{1/4} & { -1/4} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
1/2 \\
1/2 \\
\end{array}} \right]\) |
scale by \(\frac{1}{2 \sqrt 2}\), rotate by 135° |
|
\({R_3}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 1/4} & { 1/4} \\
{-1/4} & { 1/4} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
1/2 \\
1/2 \\
\end{array}} \right]\) |
scale by \(\frac{1}{2 \sqrt 2}\), rotate by −45° |
Green Boundary:
|
\({G_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{1/2} & { - 1/2} \\
{1/2} & {1/2} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
1/2 \\
-1/2 \\
\end{array}} \right]\) |
scale by \(\frac{1}{\sqrt 2}\), rotate by 45° |
|
\({G_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ - 1/4} & { - 1/4} \\
{1/4} & { - 1/4} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
1 \\
0 \\
\end{array}} \right]\) |
scale by \(\frac{1}{2 \sqrt 2}\), rotate by 135° |
|
\({G_3}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 1/4} & {1/4} \\
{-1/4} & { 1/4} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
1/2 \\
1/2 \\
\end{array}} \right]\) |
scale by \(\frac{1}{2 \sqrt 2}\), rotate by −45° |
Orange Boundary:
|
\({O_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{1/2} & { - 1/2} \\
{1/2} & {1/2} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
1/2 \\
-1/2 \\
\end{array}} \right]\) |
scale by \(\frac{1}{\sqrt 2}\), rotate by 45° |
|
\({O_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ - 1/4} & { - 1/4} \\
{1/4} & { - 1/4} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
3/4 \\
-3/4 \\
\end{array}} \right]\) |
scale by \(\frac{1}{2 \sqrt 2}\), rotate by 135° |
|
\({O_3}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 1/4} & {1/4} \\
{-1/4} & { 1/4} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
1/4 \\
-1/4 \\
\end{array}} \right]\) |
scale by \(\frac{1}{2 \sqrt 2}\), rotate by −45° |
Blue Boundary:
|
\({B_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{1/2} & { - 1/2} \\
{1/2} & {1/2} \\
\end{array}} \right]{\bf{x}} \) |
scale by \(\frac{1}{\sqrt 2}\), rotate by 45° |
|
\({B_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ - 1/4} & { - 1/4} \\
{1/4} & { - 1/4} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
1/4 \\
-1/4 \\
\end{array}} \right]\) |
scale by \(\frac{1}{2 \sqrt 2}\), rotate by 135° |
|
\({B_3}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 1/4} & {1/4} \\
{-1/4} & { 1/4} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
1/4 \\
-1/4 \\
\end{array}} \right]\) |
scale by \(\frac{1}{2 \sqrt 2}\), rotate by −45° |
which has the solution
\[x = \frac{1}{6}{\left( {54 + 6\sqrt {87} } \right)^{1/3}} - \frac{1}{{{{\left( {54 + 6\sqrt {87} } \right)}^{1/3}}}}\]The dimension of the boundary is therefore
\[d = - \frac{{\ln x}}{{\ln \sqrt 2 }} = - \frac{{\ln \left( {\frac{1}{6}{{\left( {54 + 6\sqrt {87} } \right)}^{1/3}} - \frac{1}{{{{\left( {54 + 6\sqrt {87} } \right)}^{1/3}}}}} \right)}}{{\ln \sqrt 2 }} \approx 1.523627\]
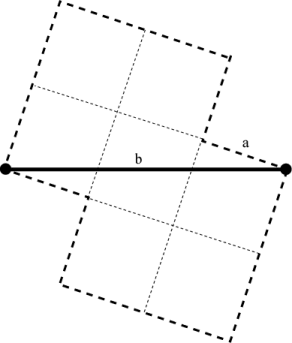
Now consider what happens with the area inside the Level 1 boundary as shown below.

The smaller red, green, blue, and orange triangles contain the same area inside the boundary and outside the boundary of Level 0. Thus in the iteration from Level 0 to Level 1, we only need to add the additional area from the light shaded regions but subtract the area from the dark shaded regions. This additional area is
\[2 \cdot \left( {\frac{1}{2} \cdot 2a \cdot a} \right) - 2 \cdot \left( {\frac{1}{2} \cdot a \cdot \frac{a}{2}} \right) = 2{a^2} - \frac{1}{2}{a^2} = \frac{3}{2}{a^2}\]The same thing will happen in the iteration from Level 1 to Level 2, except the new shaded regions would have a side that has been scaled by \(1/\sqrt 2\). Continuing the iteration and adding the additional area at each new level gives the total area inside the boundary of the twindragon to be
\[\begin{array}{l} 7{a^2} + \frac{3}{2}{a^2} + \frac{3}{2}{\left( {\frac{a}{{\sqrt 2 }}} \right)^2} + \frac{3}{2}{\left( {\frac{a}{{{{\sqrt 2 }^2}}}} \right)^2} + \frac{3}{2}{\left( {\frac{a}{{{{\sqrt 2 }^3}}}} \right)^2} + \ldots \\ \\ = 7{a^2} + \frac{3}{2}{a^2}\left( {1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \ldots } \right) \\ \\ = 7{a^2} + \frac{3}{2}{a^2}\left( {\frac{1}{{1 - \frac{1}{2}}}} \right) = 10{a^2} = b^2 \\ \end{array}\]