


\[\frac{1}{2} \cdot a \cdot \frac{{\sqrt 3 }}{2}a = \frac{{\sqrt 3 }}{4}{a^2}\]
as we can determine from the following picture

For our construction, the length of the side of the initial triangle is given by the value of s. By the result above, using a = s, the area of the initial triangle S(0) is therefore \(\dfrac{{\sqrt 3 }}{4}{s^2}\).
Area after first iteration: (using a = s/3)
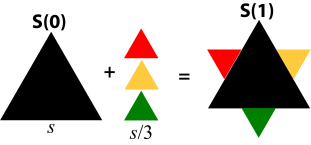
\[{\text{Area: }}\frac{{\sqrt 3 }}{4}{s^2} + 3 \cdot \frac{{\sqrt 3 }}{4}{\left( {\frac{s}{3}} \right)^2} = \frac{{\sqrt 3 }}{4}{s^2}\left( {1 + \frac{3}{9}} \right)\]
Area after second iteration: (using a = s/32)
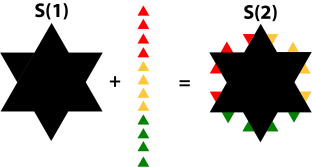
\[{\text{Area: }}\frac{{\sqrt 3 }}{4}{s^2}\left( {1 + \frac{3}{9}} \right) + 3 \cdot 4 \cdot \frac{{\sqrt 3 }}{4}{\left( {\frac{s}{9}} \right)^2} = \frac{{\sqrt 3 }}{4}{s^2}\left( {1 + \frac{3}{9} + \frac{{3 \cdot 4}}{{{9^2}}}} \right)\]
Area after third iteration: (using a = s/33)
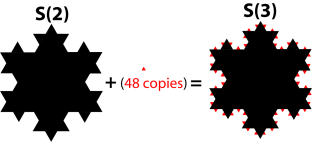
\[{\text{Area: }}\frac{{\sqrt 3 }}{4}{s^2}\left( {1 + \frac{3}{9} + \frac{{3 \cdot 4}}{{{9^2}}}} \right) + 3 \cdot 4 \cdot 4 \cdot \frac{{\sqrt 3 }}{4}\left( {\frac{s}{{{3^3}}}} \right) = \frac{{\sqrt 3 }}{4}{s^2}\left( {1 + \frac{3}{9} + \frac{{3 \cdot 4}}{{{9^2}}} + \frac{{3 \cdot {4^2}}}{{{9^3}}}} \right)\]
By now the pattern should be clear. At the kth iteration we add 3×4k-1 additional triangles of area \(\displaystyle \frac{{\sqrt 3 }}{4}{\left( {\frac{s}{{{3^k}}}} \right)^2}\). This means we add a total area of
\[3 \cdot {4^{k - 1}} \cdot \frac{{\sqrt 3 }}{4}{\left( {\frac{s}{{{3^k}}}} \right)^2} = \frac{{\sqrt 3 }}{4}{s^2}\left( {\frac{{3 \cdot {4^{k - 1}}}}{{{9^k}}}} \right)\]
to the area S(k-1) to get the area of S(k). Hence after n iterations we get the area of S(n) to be
\[\frac{{\sqrt 3 }}{4}{s^2}\left( {1 + \sum\limits_{k = 1}^n {\frac{{3 \cdot {4^{k - 1}}}}{{{9^k}}}} } \right)\]
The sum inside the parentheses is the partial sum of a geometric series with ratio r = 4/9. Therefore the sum converges as n goes to infinity, so we see that the area of the Koch snowflake is
\[\begin{align} \frac{{\sqrt 3 }}{4}{s^2}\left( {1 + \sum\limits_{k = 1}^\infty {\frac{{3 \cdot {4^{k - 1}}}}{{{9^k}}}} } \right) &= \frac{{\sqrt 3 }}{4}{s^2}\left( {1 + \frac{{3/9}}{{1 - 4/9}}} \right) \\ &= \frac{{\sqrt 3 }}{4}{s^2}\left( {\frac{8}{5}} \right) \\ &= \frac{{2\sqrt 3 }}{5}{s^2} \\ \end{align}\]

The area of the equilateral triangle inside the green section is the center equilateral triangle scaled by 1/3, so its area is 1/9. Each of the four smaller copies of the green section are a 1/3-scaled version of the entire green section, so each of them has area S/9. Therefore \[S = \frac{1}{9} + 4\cdot\frac{S}{9} \Rightarrow S = \frac{1}{5}.\] The blue and red sections outside the center equilateral triangle but inside the snowflake have the same area as the green section. Thus the area of the Koch snowflake is 1 + 3(1/5) = 8/5.
More generally, the area of the snowflake would be 8/5 times the area of the original equilateral triangle. If the length of a side of the triangle is \(s\), then the area of the triangle is \(\displaystyle \frac{\sqrt{3}}{4}s^2\) and therefore the area of the snowflake would be \[\left( {\frac{8}{5}} \right)\frac{{\sqrt 3 }}{4}{s^2} = \frac{{2\sqrt 3 }}{5}{s^2}. \]