



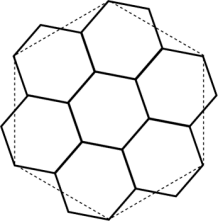
Start with a pattern of seven regular hexagons. Eight vertices are connected as shown above to create the basic red motif. The red line segments are oriented by the arrows. Now replace each red line segment by a copy of the motif scaled by r = \(1/ \sqrt 7 \) such that the copy lies to the left of the oriented edge it is replacing. Notice that this will place the copy of the motif inside the hexagon containing that edge. This recursive procedure is continued and in the limit will produce the image called William Gosper's flowsnake.
Iteration
Click the iterations to the left for an illustration of how each iteration of the flowsnake is formed from the previous iteration.

Animation
|
\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ -1/ \sqrt 14} & {3\sqrt 3 /14 } \\
{-3\sqrt 3 /14} & { -1/ \sqrt 14} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{1/14 } \\
{3\sqrt 3 /14} \\
\end{array}} \right]\) |
scale by \(1/ \sqrt{7} \), rotate by A-120° |
|
\({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 5/14} & {- \sqrt 3 / 14} \\
{ \sqrt 3 / 14} & { 5/14} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{1/14 } \\
{3\sqrt 3 /14} \\
\end{array}} \right]\) |
scale by \(1/ \sqrt{7} \), rotate by A |
|
\({f_3}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 5/14} & {- \sqrt 3 / 14} \\
{ \sqrt 3 / 14} & { 5/14} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{3/7} \\
{2 \sqrt 3 / 7} \\
\end{array}} \right]\) |
scale by \(1/ \sqrt{7} \), rotate by A |
|
\({f_4}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ -1/ \sqrt 14} & {3\sqrt 3 /14 } \\
{-3\sqrt 3 /14} & { -1/ \sqrt 14} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{11/14} \\
{5 \sqrt 3 / 14} \\
\end{array}} \right]\) |
scale by \(1/ \sqrt{7} \), rotate by A-120° |
|
\({f_5}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 5/14} & {- \sqrt 3 / 14} \\
{ \sqrt 3 / 14} & { 5/14} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{5/14} \\
{\sqrt 3 /14} \\
\end{array}} \right]\) |
scale by \(1/ \sqrt{7} \), rotate by A |
|
\({f_6}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ -2/7} & {- \sqrt 3 /7} \\
{ \sqrt 3 /7} & { -2/7} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{9/14} \\
{- \sqrt 3 / 14} \\
\end{array}} \right]\) |
scale by \(1/ \sqrt{7} \), rotate by A+120° |
|
\({f_7}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 5/14} & {- \sqrt 3 / 14} \\
{ \sqrt 3 / 14} & { 5/14} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{9/14} \\
{- \sqrt 3 / 14} \\
\end{array}} \right]\) |
scale by \(1/ \sqrt{7} \), rotate by A |

4th Iteration
There is an another way to get the flowsnake by working with hexagons directly instead of line segments. In this case start with a hexagon as shown in the figure to the right, make 7 copies scaled by r = \(1 / \sqrt 7\), rotate them by \(A = \arcsin \left( {\frac{{\sqrt 3 }}{{2\sqrt 7 }}} \right) \approx {19.1066^ \circ }\), then translate so that six of them exactly surround the seventh. This yields the following IFS [Details].
Animation
|
\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 5/ 14} & {-\sqrt 3 /14 } \\
{\sqrt 3 /14} & { 5/ 14} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{\sqrt 3 /14 } \\
{9 /14} \\
\end{array}} \right]\) |
scale by \(1/ \sqrt{7} \), rotate by A |
|
\({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 5/ 14} & {-\sqrt 3 /14 } \\
{\sqrt 3 /14} & { 5/ 14} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{5 \sqrt 3 /14} \\
{3 /14} \\
\end{array}} \right]\) |
scale by \(1/ \sqrt{7} \), rotate by A |
|
\({f_3}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 5/ 14} & {-\sqrt 3 /14 } \\
{\sqrt 3 /14} & { 5/ 14} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{2 \sqrt 3 /7} \\
{-3/ 7} \\
\end{array}} \right]\) |
scale by \(1/ \sqrt{7} \), rotate by A |
|
\({f_4}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 5/ 14} & {-\sqrt 3 /14 } \\
{\sqrt 3 /14} & { 5/ 14} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{- \sqrt 3/14} \\
{-9/ 14} \\
\end{array}} \right]\) |
scale by \(1/ \sqrt{7} \), rotate by A |
|
\({f_5}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 5/ 14} & {-\sqrt 3 /14 } \\
{\sqrt 3 /14} & { 5/ 14} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{-5 \sqrt 3 /14} \\
{-3 /14} \\
\end{array}} \right]\) |
scale by \(1/ \sqrt{7} \), rotate by A |
|
\({f_6}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 5/ 14} & {-\sqrt 3 /14 } \\
{\sqrt 3 /14} & { 5/ 14} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{-2 \sqrt 3/7} \\
{3/7} \\
\end{array}} \right]\) |
scale by \(1/ \sqrt{7} \), rotate by A |
|
\({f_7}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 5/ 14} & {-\sqrt 3 /14 } \\
{\sqrt 3 /14} & { 5/ 14} \\
\end{array}} \right]{\bf{x}}\) |
scale by \(1/ \sqrt{7} \), rotate by A |

Boundary
Animation
(one edge)
The boundary of the flowsnake can be obtained through an iterative construction that replaces the line segments forming the boundary of the hexagon used in the IFS above with the following zigzag motif, where each of the three smaller segments have been scaled by \(1 / \sqrt 7 \).
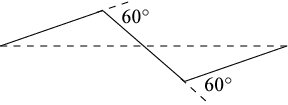
The following iterated function system would give the top right edge of the boundary. The matrix would be repeated for the other five edges with changes to the translation vectors [Details].
|
\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 5/ 14} & {-\sqrt 3 /14 } \\
{\sqrt 3 /14} & { 5/ 14} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{\sqrt 3 /14} \\
{9 /14} \\
\end{array}} \right]\) |
scale by \(1/ \sqrt{7} \), rotate by A |
|
\({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 2/ 7} & {\sqrt 3 /7 } \\
{-\sqrt 3 /7} & { 2/ 7} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{\sqrt 3 /14} \\
{9/14} \\
\end{array}} \right]\) |
scale by \(1/ \sqrt{7} \), rotate by A-60 |
|
\({f_3}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 5/ 14} & {-\sqrt 3 /14 } \\
{\sqrt 3 /14} & { 5/ 14} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{5\sqrt 3 /14} \\
{3/14} \\
\end{array}} \right]\) |
scale by \(1/ \sqrt{7} \), rotate by A |

L-System
Animation
Angle 60
Axiom F
F—>F−G−−G+F++FF+G−
G—>+F−GG−−G−F++F+G
4 iterations (initial direction 90°)
Angle 60
Axiom F+F+F+F+F+F+
F —> F−F+F
The initial direction for the L-system for the boundary of iteration \(n\) can be taken to be \(90^\circ+n\cdot A\) where \(A = \arcsin \left( {\frac{{\sqrt 3 }}{{2\sqrt 7 }}} \right) \approx {19.1066^ \circ }\).
Iteration
\[\sum\limits_{k = 1}^7 {{r^d}} = 1 \quad \Rightarrow \quad d =\frac{{\log (1/7)}}{{\log (r)}} = \frac{{\log (1/7)}}{{\log (1/ \sqrt 7)}} = 2\]
The boundary of the flowsnake is formed from six pieces, each of which is self-similar with 3 non-overlapping copies of itself, each scaled by the factor \(1/\sqrt{7}\). Therefore the boundary has a fractal dimension of \[ \frac{{\log (1/3)}}{{\log (1/\sqrt 7)}} = \frac {\log(3)}{\log( \sqrt 7)} = 1.12915 \]
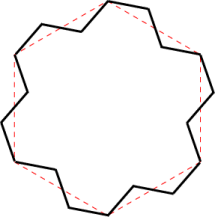 The area of the flowsnake is the same as the area of the initial hexagon. As illustrated in the figure to the right, at the first stage of the construction of the boundary, the new zigzag line segments along each edge of the initial hexagon have as much area added outside the hexagon as area is removed from inside the hexagon. Thus this first iteration has the same area as the hexagon. At each step of the iterative construction, the number of edges will continue to increase, but the same balance of adding and subtracting areas will occur, hence the total area will never change. At the limit the area enclosed by the boundary will be exactly the same as the area of the initial hexagon.
The area of the flowsnake is the same as the area of the initial hexagon. As illustrated in the figure to the right, at the first stage of the construction of the boundary, the new zigzag line segments along each edge of the initial hexagon have as much area added outside the hexagon as area is removed from inside the hexagon. Thus this first iteration has the same area as the hexagon. At each step of the iterative construction, the number of edges will continue to increase, but the same balance of adding and subtracting areas will occur, hence the total area will never change. At the limit the area enclosed by the boundary will be exactly the same as the area of the initial hexagon.
Copies of the flowsnake will tile the plane [Example]. Click for details.