Area bounded by the Koch Anti-Snowflake Curve

The first observation is that the area of a general equilateral triangle with side length a is

\[\frac{1}{2} \cdot a \cdot \frac{{\sqrt 3 }}{2}a = \frac{{\sqrt 3 }}{4}{a^2}\]

as we can determine from the following picture

For our construction, let the length of the side of the initial triangle be given by the value of s. By the result above, using a = s, the area of the initial triangle s therefore \(\frac{{\sqrt 3 }}{4}{s^2}\).

To form the Koch anti-snowflake curve, start with an equilateral triangle and begin the iteration steps for constructing a copy of the Koch curve along each of the three sides, but pointing inside the original equilateral triangle.

The areas of the newly formed equilateral triangles must be subtracted. So at the first iteration (middle figure above) we have 3 sides and along each side we remove a triangle with side length s/3. The area bounded by the curve at this iteration is therefore

\[\frac{{\sqrt 3 }}{4}{s^2} - 3 \cdot \frac{{\sqrt 3 }}{4}{\left( {\frac{s}{3}} \right)^2} = \frac{{\sqrt 3 }}{4}{s^2}\left( {1 - \frac{3}{9}} \right)\]

We have 4 new edges from each of the 3 original sides, for a total of 12 edges. Therefore at the next iteration (right figure above) we remove the areas of 12 new triangles each of which have a side of length s/9. At this iteration the area of the bounded region is

\[\frac{{\sqrt 3 }}{4}{s^2}\left( {1 - \frac{3}{9}} \right) - 3 \cdot 4 \cdot \frac{{\sqrt 3 }}{4}{\left( {\frac{s}{9}} \right)^2} = \frac{{\sqrt 3 }}{4}{s^2}\left( {1 - \frac{3}{9} - \frac{{3 \cdot 4}}{{{9^2}}}} \right)\]

Continuing with the construction, at the kth iteration we remove 3×4^k-1 additional triangles of area \(\frac{{\sqrt 3 }}{4}{\left( {\frac{s}{{{3^k}}}} \right)^2}\). The total area that must be subtracted is

\[3 \cdot {4^{k - 1}} \cdot \frac{{\sqrt 3 }}{4}{\left( {\frac{s}{{{3^k}}}} \right)^2} = \frac{{\sqrt 3 }}{4}{s^2}\left( {\frac{{3 \cdot {4^{k - 1}}}}{{{9^k}}}} \right)\]

Hence after n iterations the area of the bounded region is

\[\frac{{\sqrt 3 }}{4}{s^2}\left( {1 - \sum\limits_{k = 1}^n {\frac{{3 \cdot {4^{k - 1}}}}{{{9^k}}}} } \right)\]

The sum inside the parentheses is the partial sum of a geometric series with ratio r = 4/9. Therefore the sum converges as n goes to infinity, so we see that the area bounded by the Koch anti-snowflake curve is

\[\begin{align} \frac{{\sqrt 3 }}{4}{s^2}\left( {1 - \sum\limits_{k = 1}^\infty {\frac{{3 \cdot {4^{k - 1}}}}{{{9^k}}}} } \right) &= \frac{{\sqrt 3 }}{4}{s^2}\left( {1 - \frac{{3/9}}{{1 - 4/9}}} \right) \\ &= \frac{{\sqrt 3 }}{4}{s^2}\left( {\frac{2}{5}} \right) \\ \end{align}\]

Since \(\frac{{\sqrt 3 }}{4}{s^2}\) is the area of the original equilateral triangle, this shows that the bounded region has area equal to 2/5 that of the original triangle.

Suppose that the area of the initial equilateral triangl is 1. Let S be the area inside the part of the snowflake outlined by the red Koch curve and the side of the triangle in the following image.

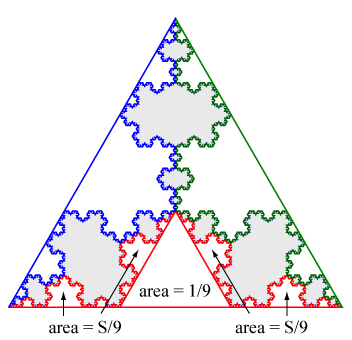
The area of the equilateral triangle inside the red section is the initial equilateral triangle scaled by 1/3, so its area is 1/9. Each of the four smaller copies of the red section are a 1/3-scaled version of the entire red section by the self-similarity of the Koch curve, so each of them has area S/9. Therefore \[S = \frac{1}{9} + 4\cdot\frac{S}{9} \Rightarrow S = \frac{1}{5}.\] The blue and green sections inside the initial equilateral triangle but outside the anti-snowflake have the same area as the red section. These areas must be subtracted, so the area of the Koch anti-snowflake is 1 - 3(1/5) = 2/5.

More generally, the area of the anti-snowflake would be 2/5 times the area of the original equilateral triangle.