


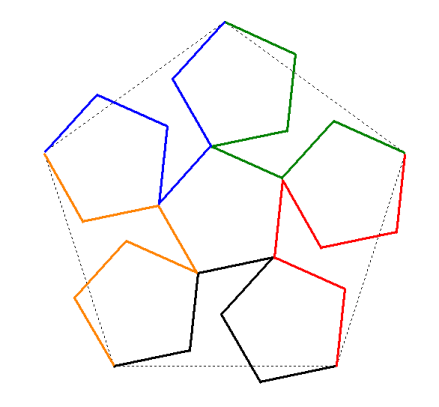
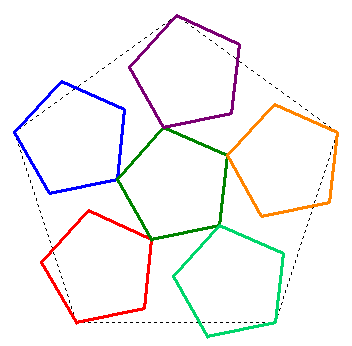
You can also see how five copies of the pentadentrite fit together by successively adding copies using the buttons below, or by viewing the L-system animation farther down.

|
\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{0.341} & { - 0.071} \\
{0.071} & {0.341} \\
\end{array}} \right]{\bf{x}}\)
|
scale by r, rotate by 11.82° |
|
\({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{0.341} & { - 0.071} \\
{0.071} & {0.341} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{0.649} \\
{0.136} \\
\end{array}} \right]\)
|
scale by r, rotate by 11.82° |
|
\({f_3}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{0.341} & { - 0.071} \\
{0.071} & {0.341} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{0.071} \\
{0.659} \\
\end{array}} \right]\)
|
scale by r, rotate by 11.82° |
|
\({f_4}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{0.341} & { - 0.071} \\
{0.071} & {0.341} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{-0.604} \\
{0.271} \\
\end{array}} \right]\)
|
scale by r, rotate by 11.82° |
|
\({f_5}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{0.341} & { - 0.071} \\
{0.071} & {0.341} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{-0.445} \\
{-0.491} \\
\end{array}} \right]\)
|
scale by r, rotate by 11.82° |
|
\({f_6}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{0.341} & { - 0.071} \\
{0.071} & {0.341} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{0.330} \\
{ - 0.575} \\
\end{array}} \right]\)
|
scale by r, rotate by 11.82° |

\[\sum\limits_{k = 1}^6 {{r^d}} = 1 \quad \Rightarrow \quad d = \frac{{\log (1/6)}}{{\log (r )}} = 1.6995\]
Angle 72
Axiom F+F+F+F+F
F —> F+F−F−−F+F+F
4 iterations