


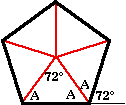
First some facts about the angles in a pentagon. Connect the center of the pentagon to each of the five vertices, forming five equivalent isosceles triangles. The measure of each of the central angles is 360°/5 = 72°. Let A be the measure of the other two angles in the isosceles triangles. Then A+A+72=180. This means that the measure of the exterior angle at each vertex is also 72°.
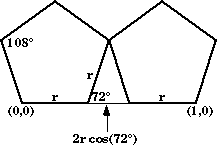
Assume that the initial pentagon P(0) is positioned with its bottom edge having vertices at (0,0) and (1,0). The figure shows two of the scaled pentagons of P(1) with base along the x-axis. These pentagons form an isosceles triangle with base angle 72°. The length of the base is therefore 2*r*cos(72°). Because the total length of the base of the pentagons and the base of the triangle must be the same as the length of the base of P(0), we see that
\[2r + 2r\cos {72^ \circ } = 1 \quad \Rightarrow \quad r = \frac{1}{{2 + 2\cos {{72}^ \circ }}} = \frac{1}{{2\left( {1 + \frac{{\sqrt 5 - 1}}{4}} \right)}} = \frac{2}{{3 + \sqrt 5 }}\]
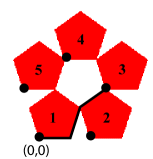
The translation of pentagon 2 is easy since that pentagon is just translated to the right by 1-r = 0.618. The easiest way to compute how each of the other scaled pentagons must be translated is to use vectors. For example, the three vectors illustrated in black in the above picture show how the lower left corner of pentagon 3 is translated from the origin. Using the angles from the figure below, we get
\[(r,0) + (r\cos {72^ \circ },r\sin {72^ \circ }) + (r\cos {36^ \circ },r\sin {36^ \circ }) = (0.809,0.588)\]

For the other two we have
Pentagon 4:
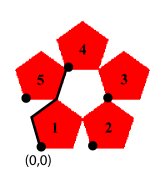
\(( - r\cos {72^ \circ },r\sin {72^ \circ }) + (r\cos {36^ \circ },r\sin {36^ \circ }) + (r\cos {72^ \circ },r\sin {72^ \circ }) = (0.309,0.951)\)
Pentagon 5:
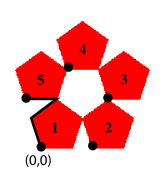
\(( - r\cos {72^ \circ },r\sin {72^ \circ }) + (r\cos {36^ \circ },r\sin {36^ \circ }) + ( - r,0) = ( - 0.191,0.588)\)