

|
\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{0.309} & { - 0.255} \\
{0.255} & {0.309} \\
\end{array}} \right]{\bf{x}}\)
|
scale by r, rotate by 36° |
|
\({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{0.309} & { - 0.254} \\
{0.254} & {0.309} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{0.727} \\
{0} \\
\end{array}} \right]\)
|
scale by r, rotate by 36° |
|
\({f_3}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{0.309} & { - 0.255} \\
{0.255} & {0.309} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{0.225} \\
{0.691} \\
\end{array}} \right]\)
|
scale by r, rotate by 36° |
|
\({f_4}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{0.309} & { - 0.255} \\
{0.255} & {0.309} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{-0.588} \\
{0.427} \\
\end{array}} \right]\)
|
scale by r, rotate by 36° |
|
\({f_5}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{0.309} & { - 0.255} \\
{0.255} & {0.309} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{-0.588} \\
{-0.427} \\
\end{array}} \right]\)
|
scale by r, rotate by 36° |
|
\({f_6}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{0.309} & { - 0.255} \\
{0.255} & {0.309} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{0.225} \\
{ -0.691} \\
\end{array}} \right]\)
|
scale by r, rotate by 36° |
Start with a pentagon inscribed in the unit circle as shown in the figure below. The 6 smaller pentagons are each scaled by the factor \(r = \frac{3-\sqrt 5}{2} = 0.38197 \) and rotated by the angle A = 36°. The red pentagon does not need to be translated, but each of the other 5 scaled and rotated pentagons needs to be translated so that the appropriate vertex is translated back to the corresponding vertex in the original pentagon, as shown in the figure.
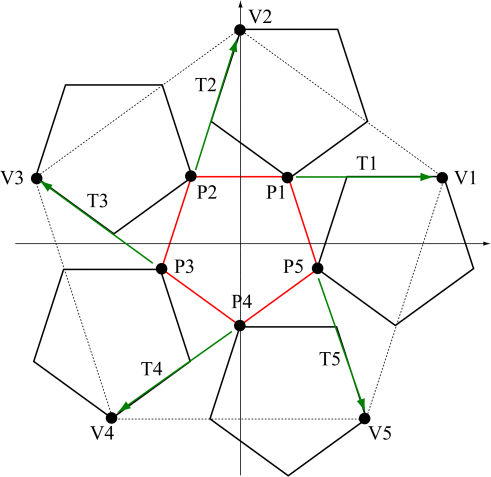
To find the translation vectors, we just need to compute \({T_i} = {V_i} - {P_i} = {V_i} - M{V_i}\) where \[{V_i} = \left[ {\begin{array}{*{20}{c}} {\cos \left( {{{18}^ \circ } + {{72}^ \circ } \cdot (i - 1)} \right)} \\ {\sin \left( {{{18}^ \circ } + {{72}^ \circ } \cdot (i - 1)} \right)} \\ \end{array}} \right]\] for i = 1, 2, 3, 4, 5. This gives
\({T_1} = \left[ {\begin{array}{*{20}{c}} {\cos {{18}^ \circ }} \\ {\sin {{18}^ \circ }} \\ \end{array}} \right] - M\left[ {\begin{array}{*{20}{c}} {\cos {{18}^ \circ }} \\ {\sin {{18}^ \circ }} \\ \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {0.72654} \\ {0} \\ \end{array}} \right]\)
\({T_2} = \left[ {\begin{array}{*{20}{c}} {\cos {{90}^ \circ }} \\ {\sin {{90}^ \circ }} \\ \end{array}} \right] - M\left[ {\begin{array}{*{20}{c}} {\cos {{90}^ \circ }} \\ {\sin {{90}^ \circ }} \\ \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {0.22451} \\ {0.69098} \\ \end{array}} \right]\)
\({T_3} = \left[ {\begin{array}{*{20}{c}} {\cos {{162}^ \circ }} \\ {\sin {{162}^ \circ }} \\ \end{array}} \right] - M\left[ {\begin{array}{*{20}{c}} {\cos {{162}^ \circ }} \\ {\sin {{162}^ \circ }} \\ \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - 0.58779} \\ {0.42705} \\ \end{array}} \right]\)
\({T_4} = \left[ {\begin{array}{*{20}{c}} {\cos {{234}^ \circ }} \\ {\sin {{234}^ \circ }} \\ \end{array}} \right] - M\left[ {\begin{array}{*{20}{c}} {\cos {{234}^ \circ }} \\ {\sin {{234}^ \circ }} \\ \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - 0.58779} \\ { - 0.42705} \\ \end{array}} \right]\)
\({T_5} = \left[ {\begin{array}{*{20}{c}} {\cos {{306}^ \circ }} \\ {\sin {{306}^ \circ }} \\ \end{array}} \right] - M\left[ {\begin{array}{*{20}{c}} {\cos {{306}^ \circ }} \\ {\sin {{306}^ \circ }} \\ \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {0.22451} \\ { - 0.69098} \\ \end{array}} \right]\)