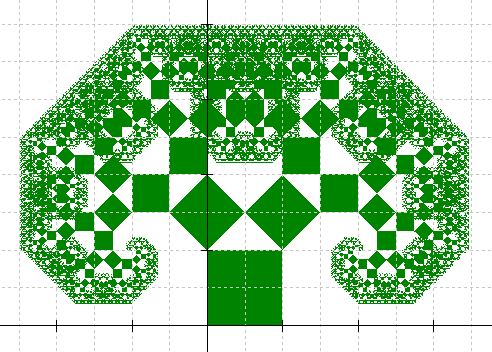
Each time we iterate the squares are scaled by a factor of \(\sqrt{2}/2\). Notice how the squares alternate in direction. To find the total height we must take either the height of a square or the length of a diagonal and add them all together. This gives
\[1 + \sqrt 2 \cdot \left( {\frac{{\sqrt 2 }}{2}} \right) + {\left( {\frac{{\sqrt 2 }}{2}} \right)^2} + \sqrt 2 \cdot {\left( {\frac{{\sqrt 2 }}{2}} \right)^3} + {\left( {\frac{{\sqrt 2 }}{2}} \right)^4} + \sqrt 2 \cdot {\left( {\frac{{\sqrt 2 }}{2}} \right)^5} + \ldots \]This sum consists of two geometric series each with common ratio \({\left( {\sqrt 2 /2} \right)^2} = 1/2\), so the total height is
\[\frac{1}{{1 - \frac{1}{2}}} + \sqrt 2 \cdot \left( {\frac{{\sqrt 2 }}{2}} \right) \cdot \frac{1}{{1 - \frac{1}{2}}} = 2 + 2 = 4\]Now for the width we would have the figure below.
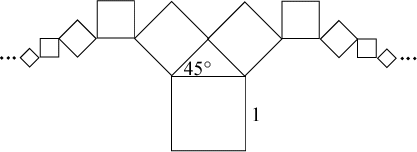
Using symmetry, we want to calculate only the width for the squares going to the right. We do not include the initial square. Thus this half-width would be given by
\[\sqrt 2 \cdot \left( {\frac{{\sqrt 2 }}{2}} \right) + {\left( {\frac{{\sqrt 2 }}{2}} \right)^2} + \sqrt 2 \cdot {\left( {\frac{{\sqrt 2 }}{2}} \right)^3} + {\left( {\frac{{\sqrt 2 }}{2}} \right)^4} + \sqrt 2 \cdot {\left( {\frac{{\sqrt 2 }}{2}} \right)^5} + \ldots \]This is the same sum as the one above except without the initial 1, and so the half-width is equal to 3. The total width is therefore 6. The tree fits into the rectangle −2.5 ≤ x ≤ 3.5 by 0 ≤ y ≤ 4.