Details about the Bottom of a Symmetric Binary Tree

Let the tree be defined by the angle θ and scaling factor r. We will take the base of the tree to be at the origin and the initial vertical trunk to be of length 1. By the "bottom" of the tree we will mean the bottom of the branch tips, that is, the smallest y-coordinate of the branch tips.

Let \(\alpha\) be the complex number \(\alpha = e^{\theta i}=\cos{\theta} + i \sin{\theta}\). We can represent the trunk of the tree by the complex number \(i\) (which we can also think of geometrically as a vector). Recall that multiplying a vector by r will scale the vector by r, that multiplying the vector by \(\alpha\) corresponds to a counterclockwise rotation by θ, and multiplying by \(\alpha^{-1}\) corresponds to a clockwise rotation by θ. We also have \(\alpha^n = e^{n\theta i}=\cos{(n\theta)} + i \sin{(n\theta)}\) and \(\alpha^{-n} = e^{-n\theta i}=\cos{(n\theta)} - i \sin{(n\theta)}\) for all integers n.

To get to the bottom of the branch tips, we need the initial branches to turn right until the last branch passes the vertical downward direction. We then want to go vertically downward as much as possible for each new branch in the construction of the tree. Thus we want to alternate left and right branches. This gives the path R^k(LR)^∞, where k is the smallest integer such that kθ ≥ 180°. In terms of the complex numbers, this means we want to multiply by \(\alpha^{-1}\) for the first k branches, then alternate multiplying the vectors representing the branches by \(\alpha\) and \(\alpha^{-1}\), while at the same time also multiplying by r. The branch tip for this path is therefore located at the point \((x,y)\) corresponding to the complex number

\( \left(i + i r \alpha^{-1} + i r^2 \alpha^{-2} + \ldots + i r^k \alpha^{-k}\right) + i r^k \alpha^{-k} \cdot \left( {r \alpha + r^2 + r^3 \alpha + r^4 + \dots} \right) \) \[ \begin{align} &= i \left( \sum_{n=0}^{k}{r^n \alpha^{-n}} + r^k \alpha^{-k} \cdot \left( \dfrac{ra}{1-r^2} + \frac{r^2}{1-r^2} \right) \right) \\ \\ &= i \left( \sum_{n=0}^{k}{r^n \alpha^{-n}} + \frac{r^{k+1}\alpha^{-(k-1)} + r^{k+2}\alpha^{-k}}{1-r^2} \right) = iz. \end{align} \]

The y-coordinate of this branch tip is \(\text{Im}(iz) = \text{Re}(z)\), or

\[ \sum_{n=0}^{k}{r^n \cos(n \theta)} + \frac{r^{k+1} \cos((k-1)\theta) + r^{k+2} \cos(k \theta)}{1-r^2}. \] Here is an example with θ = 55°, so k = 4. The image on the left shows the R⁴(LR)^∞ path while the image on the right shows the actual tree. The y-coordinate of the R⁴(LR)^∞ branch tip is y = 0.53212.

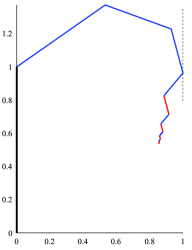
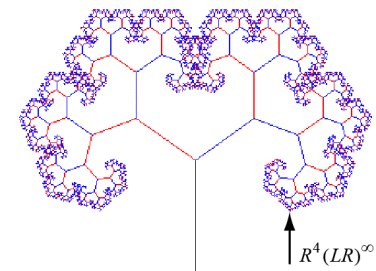
R⁴(LR)^∞ path, θ = 55°, r = 0.65

The following image shows the symmetric binary tree for θ = 160° and r = 0.8 along with the path R⁴(LR)^∞. The smallest integer satisfying kθ ≥ 180° is k = 2, so this example shows that the path described above will not always produce the branch tip with the smallest y-coordinate. Here the R²(LR)^∞ branch tip has y = 0.27365 while the R⁴(LR)^∞ branch tip is at y = 0.22498.

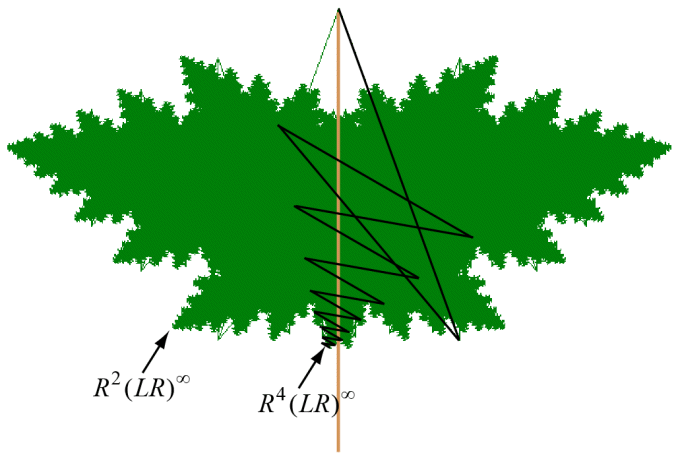
θ = 160°, r = 0.8

In this case the black path is of the form R^m(LR)^∞ where m is the smallest integer satisfying mθ ≥ 540°. In essence, the black path starts with enough right turns until the last branch has passed the downward vertical direction for the second time before it begins to alternate between left and right branch turns.

Let y_n be the y-coordinate of the Rⁿ(LR)^∞ branch tip. For a fixed θ, this coordinate depends on the value of r. Let k be the smallest integer satisfying kθ ≥ 180° and let m be the smallest integer satisfying mθ ≥ 540°. Let \(f_\theta (r)=y_m - y_k\) be the difference between the y-coordinates of the two corresponding branch tips , so \[ \begin{align} f_\theta (r) &= \sum_{n={k+1}}^{m}{r^n \cos(n \theta)} \\ \\ &+ \frac{r^{m+1} \cos((m-1)\theta) + r^{m+2} \cos(m \theta) - r^{k+1} \cos((k-1)\theta) - r^{k+2} \cos(k \theta)}{1-r^2} \end{align} \] If \(f_\theta (r)\) is positive then y_k is less than y_m, but if \(f_\theta (r)\) is negative then y_k is greater than y_m.

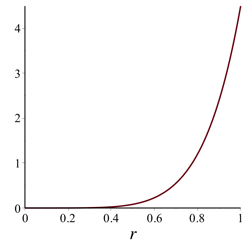
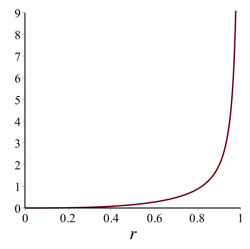
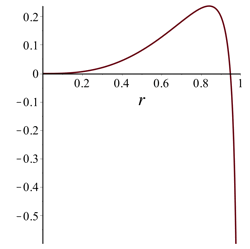
Note that \(f_\theta (0) = 0\). It can be shown [Details] that for r close to 0, the graph of \(f_\theta (r)\) will initially begin increasing in a concave up fashion as r increases, and thus \(f_\theta (r)\) will be positive for r close to 0. Below are examples of the three things that can happen with the graph of \(f_\theta (r)\) for 0 < r < 1:

θ = 60° \(\lim_{r \rightarrow 1^{-}} f_\theta (r) = A_\theta > 0\)	θ = 135° \(\lim_{r \rightarrow 1^{-}} f_\theta (r) = +\infty\)	θ = 146° \(\lim_{r \rightarrow 1^{-}} f_\theta (r) = -\infty\)

To see why, we need to examine the behavior of the numerator of the fraction in the expression for \(f_\theta (r)\) when r = 1 since the denominator is positive and goes to 0 as r approaches 1 from the left. So we need to determine the sign of \[ N(\theta) = \cos((m-1)\theta) + \cos(m \theta) -\cos((k-1)\theta) -\cos(k \theta) \] where \(k = \lceil \frac{180}{\theta}\rceil\) and \(m = \lceil \frac{540}{\theta} \rceil\), in particular whether N(θ) is 0, positive, or negative (corresponding to the three graphs above).

Below is the graph of \(N(\theta)\) showing that \(N(\theta)\) alternates between intervals where it is positive and intervals where it is negative (with those intervals getting smaller and alternating more rapidly as θ approaches 0.)

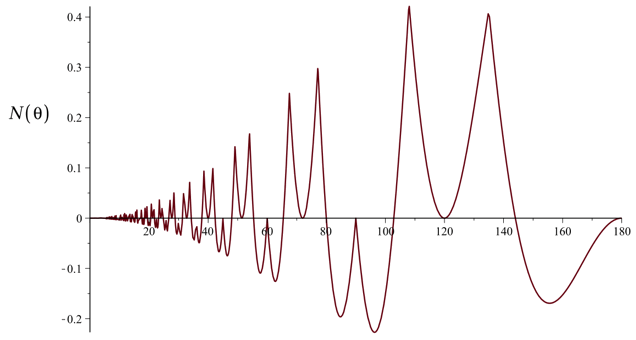
Here are closer views of the graph on the intervals 40° ≤ θ ≤ 90° and 90° ≤ θ ≤ 180°.

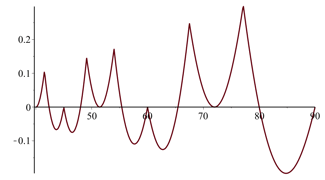
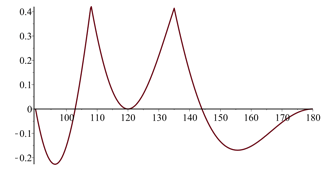
The places where the graph has a sharp corner are where \(\theta = \dfrac{540^\circ}{p}\) for an integer p ≥ 4.

The zeros of N(θ) occur at \(\theta = \dfrac{720^\circ}{p}\) for all integers p ≥ 4 [Proof]. Starting at the right end of the graph and going in decreasing order, the first four zeros are at 180°, 144°, 120°, and 102.85714°.

If θ is a zero of N(θ), then \(\lim_{r \rightarrow 1^{-}} f_\theta (r)\) exists and is positive [Proof]. Where N(θ) is positive we have \(\lim_{r \rightarrow 1^{-}} f_\theta (r) = +\infty\). For these values of θ, therefore, \(f_\theta (r) > 0\) for all 0 < r < 1 and hence y_k will be less than y_m.

The intervals where N(θ) is negative are of the form

\[ \frac{720^\circ}{4n+5} < \theta < \frac{720^\circ}{4n+4} \text{ and } \frac{720^\circ}{4n+4} < \theta < \frac{720^\circ}{4n+3} \] for \(n = 0,1,2, \ldots\). (For n = 0, only the first interval is used. This gives \(144^\circ < \theta < 180^\circ\).)

On these intervals, we have \(f_\theta (r)\) positive for small r and \(\lim_{r \rightarrow 1^{-}} f_\theta (r) = -\infty\), so there must be some some r_B between 0 and 1 where \(f_\theta (r_B) = 0.\)

The equation \(f_\theta (r) = 0\) can be solved numerically to find the solution r_B. This equation will also have a solution on the intervals where N(θ) is positive, but for those values of θ, r_B will be greater than 1. The next two figures show the graph of r_B for 0° < θ < 180°, and a close up of this graph just on the range 30° < θ < 102.85714° (= 720°/7).

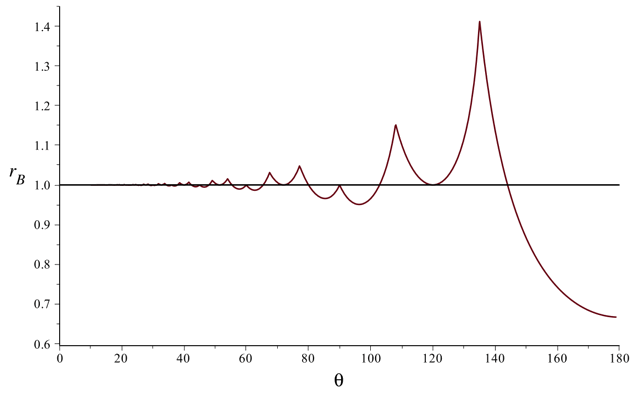
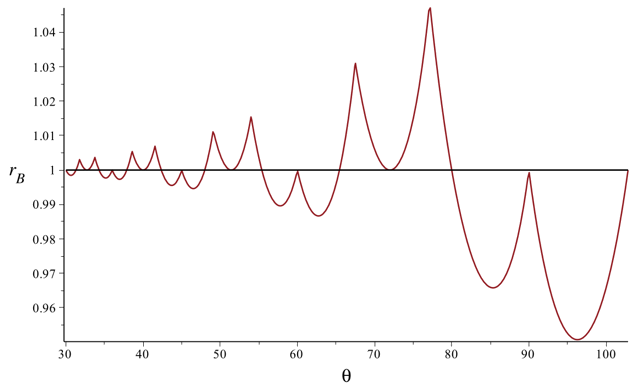
The intervals where N(θ) < 0 correspond to the intervals in these graphs where r_B < 1. On these intervals, the bottom of the symmetric binary tree will be y_m instead of y_k for r_B < r < 1.

Notice, however, that when θ < 102.85714°, the value of the critical scaling factor r_B is greater than 0.95 so that for all practical purposes the bottom of a "reasonable" symmetric binary tree will be determined by the R^k(LR)^∞ path. Any choice of r > 0.95 will produce a tree that has a massive overlap of branches. Only on the interval θ > 144° is there an opportunity for r_B to be small enough that one can generate an interesting tree (see, for example, the tree above with θ = 160° and r = 0.8.) We actually have \[ r_B = \frac{2\cos(\theta)}{1-4\cos^2 (\theta)} \] for θ > 144° [Maple Calculation]. So r_B converges to 2/3 as θ approaches 180°.