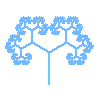

For 120° < θ < 180°, for which k = 3, we have
\[ \begin{align} f_\theta (r) &= 1 + r\cos ( {{{\theta}}} ) + {r^2}\cos ( {2{{\theta}}} ) + {r^3}\cos ( {3{{\theta}}} ) + \frac{{{r^4}\cos ( {2{{\theta}}} ) + {r^5}\cos ( {3{{\theta}}} ) - 1 - r\cos ( {{{\theta}}} )}}{{1 - {r^2}}} \\ \\ &= \frac{{ - 2{r^2}\sin^2 {{( {{{\theta}}} )}}( {2r\cos ( {{{\theta}}} ) + 1} )}}{{1 - {r^2}}} = 0 \\ \\ &\Rightarrow 2r\cos ( {{{\theta}}} ) + 1 = 0 \\ \\ &\Rightarrow r_\theta = -\frac{1}{2\cos(\theta)}. \end{align} \] For 90° < θ < 120°, for which k = 4, we have \[ \begin{align} f_\theta (r) &= 1 + r\cos ( {{{\theta}}} ) + {r^2}\cos ( {2{{\theta}}} ) + {r^3}\cos ( {3{{\theta}}} ) + {r^4}\cos ( {4{{\theta}}} ) + \frac{{{r^5}\cos ( {3{{\theta}}} ) + {r^6}\cos ( {4{{\theta}}} ) - 1 - r\cos ( {{{\theta}}} )}}{{1 - {r^2}}} \\ \\ &= \frac{{ - 2{r^2}\sin^2 {{( {{{\theta}}} )}}( {4{r^2}\cos^2 {{( {{{\theta}}} )}} + 2r\cos ( {{{\theta}}} ) - {r^2} + 1} )}}{{1 - {r^2}}} = 0 \\ \\ &\Rightarrow {r^2}(4\cos^2 {( {{\theta}} )} - 1) + 2r\cos ( {{\theta}} ) + 1 = 0 \\ \\ &\Rightarrow r_\theta = - \frac{{\cos ( {{{\theta}}} ) + \sqrt { - 3\cos^2 {{( {{{\theta}}} )}} + 1} }}{{4\cos^2 {{( {{{\theta}}} )}} - 1}}. \end{align} \] [Maple Calculations]