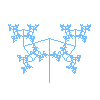
Golden 108° Symmetric Binary Tree
Taylor observed that five copies of a golden 108° symmetric binary tree can be placed inside a pentagon in such a way that the trees touch but do not overlap. The pentagon has edges of length \(\sqrt{58-31\phi} \approx 2.80017\) when the trunk of each tree is of length 1. Click on the buttons to the left to fit the five copies inside this pentagon. Each tree has its trunk positioned at the vertex of a smaller pentagon with side length \(\sqrt{7-4\phi} \approx 0.72654.\) Each tree is rotated 72° clockwise around the center of the pentagon. The trees intersect at five branch tips. [
Details]
Five copies of the golden 108° will also fit around the outside of a pentagon with sides of length \(\sqrt{\phi+2} \approx 1.90211\) in such a way that the top edge of one tree is collinear with the side edges of the trees on either side. The base of the trunk of each tree lie at the vertices of a pentagon with sides of length \(\sqrt{4\phi+3} \approx 3.07768\) when each trunk is of length 1.
If the top edges of the five trees are extended until they meet, the result will be a pentagram in which each tree will fit inside a golden isosceles triangle (72°-72°-36°) attached to an edge of the pentagon. [Details]