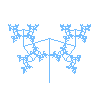

\[ \begin{array}{ll} \sin(18^\circ) = \dfrac{\sqrt{5}-1}{4} & \cos(18^\circ) = \sqrt{\dfrac{5+\sqrt{5}}{8}} \\ \sin(36^\circ) = \sqrt{\dfrac{5-\sqrt{5}}{8}} & \cos(36^\circ) = \dfrac{\sqrt{5}+1}{4} \\ \sin(108^\circ) = \sqrt{\dfrac{5+\sqrt{5}}{8}} & \cos(108^\circ) = \dfrac{1-\sqrt{5}}{4} \end{array} \]
We have
\[ \alpha = \cos(108^\circ) + i \sin(108^\circ) \quad k = \cos(18^\circ) + i \sin(18^\circ) \quad S = \sqrt{7-4\phi}\left(\cos(36^\circ) - i \sin(36^\circ)\right)\] with \(\sqrt{7-4\phi} = \sqrt{5-2\sqrt{5}}\).
With the help of the computer algebra system Maple, we find that the branch tip for the green R2(LR)∞ path then corresponds to the complex number \[A = i + i\alpha^{-1} + i r \alpha^{-2}= \frac{1}{8}\left(\sqrt{5}-1\right)\sqrt{10+2\sqrt{5}} + i \left(\frac{3}{4}-\frac{1}{4}\sqrt{5}\right)\] and the the branch tip for the red path L2(RL)∞ is \[B = S + k + k\alpha + kr\alpha^2 = \frac{1}{4}\left(\sqrt{5}+1\right)\sqrt{5-2\sqrt{5}} + i \left(\frac{3}{4}-\frac{1}{4}\sqrt{5}\right)\]
We need to show that the real parts of A and B are the same. To do this we need several facts about the golden ratio \(\phi\).
\[ \frac{\sqrt{5}-1}{2} = \frac{1}{\phi}=\phi-1 \quad\quad \frac{\sqrt{5}+1}{2}=\phi \quad \quad \frac{1}{\phi^2} = 2-\phi \quad \quad \phi^2 = \phi+1 \quad \quad \phi^3 = 2\phi+1 \] Therefore \[ \begin{array}{lcl} \frac{1}{8}\left(\sqrt{5}-1\right)\sqrt{10+2\sqrt{5}} & \quad \quad & \frac{1}{4}\left(\sqrt{5}+1\right)\sqrt{5-2\sqrt{5}} \\ = \frac{1}{4\phi}\sqrt{10+2\sqrt{5}} & \quad\quad & =\frac{1}{2}\phi\sqrt{5-2\sqrt{5}} \\ = \frac{1}{2\phi}\sqrt{2+\phi} & \quad\quad & = \frac{1}{2}\phi\sqrt{7-4\phi} \\ = \frac{1}{2}\sqrt{\frac{2}{\phi^2}+\frac{1}{\phi}} & \quad\quad & = \frac{1}{2}\sqrt{7\phi^2-4\phi^3} \\ = \frac{1}{2}\sqrt{4-2\phi+\phi-1} & \quad\quad & =\frac{1}{2}\sqrt{7\phi+7-8\phi-4} \\ = \frac{1}{2}\sqrt{3-\phi} & \quad\quad & =\frac{1}{2}\sqrt{3-\phi} \end{array} \]
This shows that A = B and that the two branch tips are the same point.
[Maple Calculations]