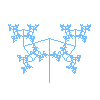



The dotted regular pentagon in the figure above has its top vertex placed at the origin and has sides of length \(\sqrt{7-4\phi} = \sqrt{5-2\sqrt{5}}.\) The green golden 108° tree is placed with the base of its trunk at this top vertex. Rotate the green tree by 72° clockwise and move the base of its trunk to the next vertex (in the clockwise direction). We claim that the branch tip of the path R2(LR)∞ for the green tree will coincide with the branch tip of the path L2(RL)∞ for the red tree.
Let \(\alpha = e^{108^\circ i}\). This complex number represents a counterclockwise rotation of 108°. The complex number \(\alpha^{-1}\) represents to a clockwise rotate of 108°.
The vector for the trunk of the green tree can be taken to be the complex number i. The branch tip for the green R2(LR)∞ path then corresponds to the complex number \[ \begin{align} i &+ ir\alpha^{-1} + ir^2\alpha^{-2} + ir^3\alpha^{-1} + ir^4\alpha^{-2} + ir^5\alpha^{-1} + \cdots \\ \\ &= i + \frac{ir\alpha^{-1}}{1-r^2} + \frac{ir^2\alpha^{-2}}{1-r^2} \\ \\ &= i + i\alpha^{-1} + i r \alpha^{-2} \\ \\ &= 0.58778525+0.19098301i \end{align} \] The vector for the trunk of the red tree can be represented by the complex number \( k=\cos(18^\circ) + i\sin(18^\circ)\). The vector S from the trunk of the green tree to the trunk of the red tree is given (as a complex number) by \(S = \sqrt{7-4\phi}\left(\cos(36^\circ) - i\sin(36^\circ)\right).\) The branch tip for the red path L2(RL)∞ is therefore \[ \begin{align} S &+ k + kr\alpha + kr^2\alpha^2 + kr^3\alpha + kr^4\alpha^2 + kr^5\alpha + \cdots \\ \\ &= S + k + \frac{kr\alpha}{1-r^2} + \frac{kr^2\alpha^2}{1-r^2} \\ \\ &= S + k + k\alpha + kr\alpha^2 \\ \\ &= 0.58778525+0.19098301i \end{align} \] So the two branch tips are the same and the claim is verified [See symbolic derivation].
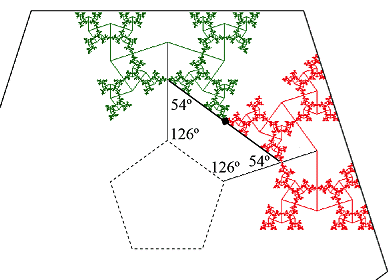
The top edge of the green subtree whose trunk is the last branch of the path RR makes an angle of 54° with the main trunk [Proof]. The same is true of the top edge of the red subtree whose trunk is the last branch of the path LL. These two edges both contain the same point as shown above. Because the two trunks both make the same angle of 126° with the side of the pentagon, and the sum of those four angles is 360°, the green and red edges must form a straight line segment (angle of 180° at the intersection point) since the sum of the interior angles of a pentagon is 540°.
By symmetry the same thing will happen with all the other golden 108° trees placed around the pentagon whose vertices are the trunks of the trees. In particular, this means that the five trees both lie around the outside of an inner pentagon as well as inside of a larger outer pentagon.
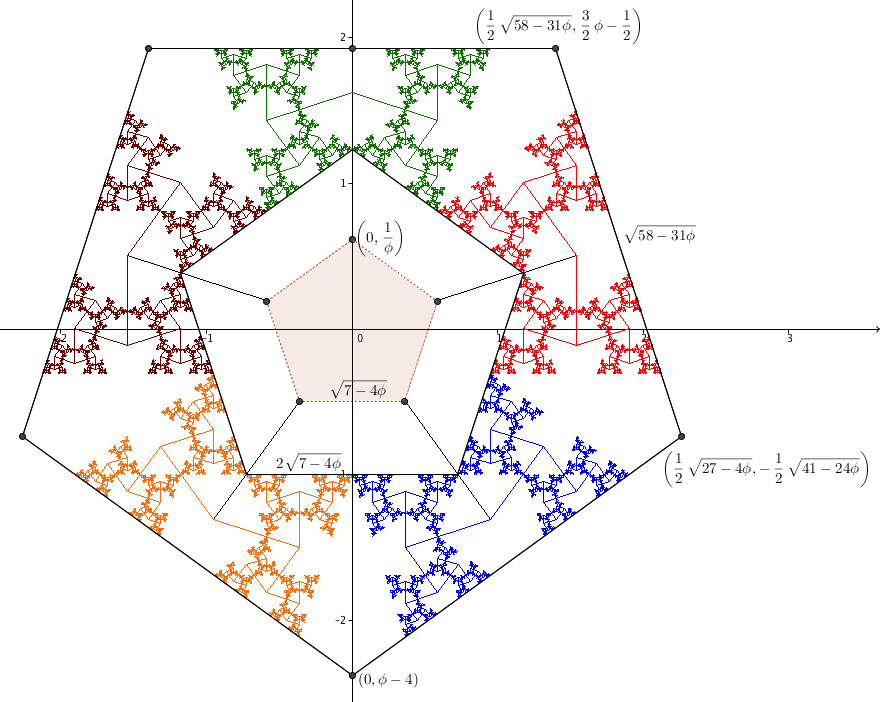
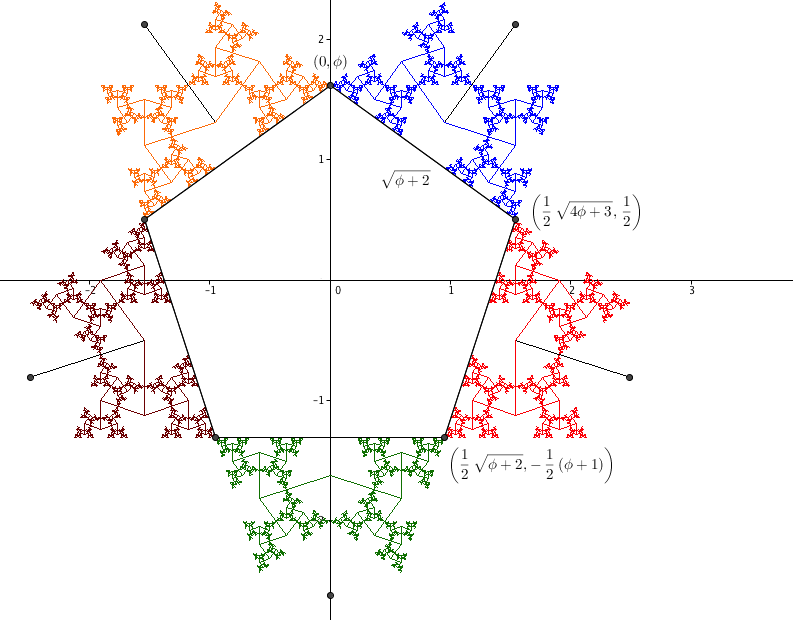
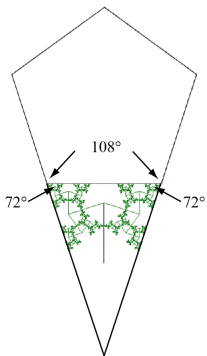
The interior angles of a regular pentagon are each equal to 108°. The side edges of the golden 108° tree makes an angle of 72° with the top edge [Proof]. Because those two angles add to 180°, the side edges of the tree align with the corresponding edges of the pentagon. If the edges of the pentagon are extended until they meet, the result will be a golden triangle with angles 72°-72°-36° that contains the golden 108° tree. The same thing will happen for all five edges of the pentagon, forming a pentagram.
