


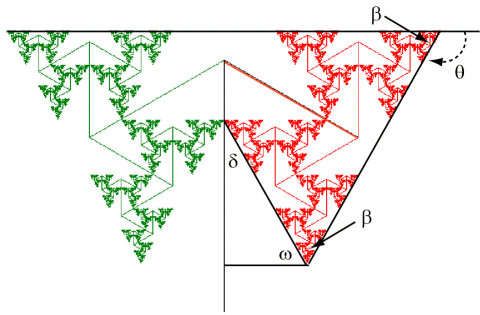
Let θ = 120°. The red subtree whose trunk starts at the top of the main tree's trunk is a scaled version of the main tree. It has been rotated by θ and therefore the top edge of the main tree is also rotated by θ to become the top edge of the red subtree (and also scaled by r). Therefore angle β = 180° − θ = 60°.
We also have ω + β = θ and so ω = θ − β = 2θ − 180°. Hence δ = 90° − ω = 270° − 2θ. For the golden 120° tree, therefore, δ = 30°.
(Note: These calculations for the angles work for any self-contacting symmetric binary tree with 90° ≤ θ ≤ 135°.)