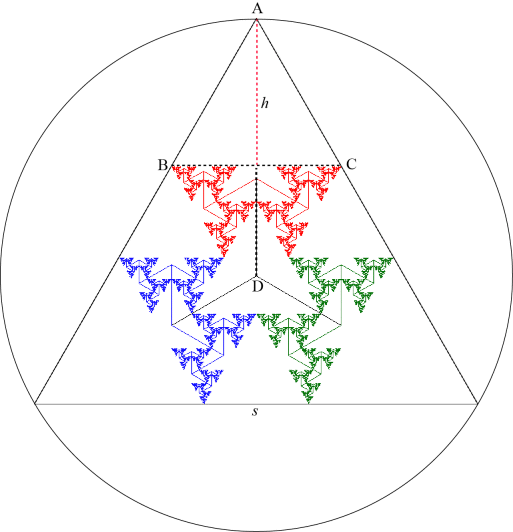
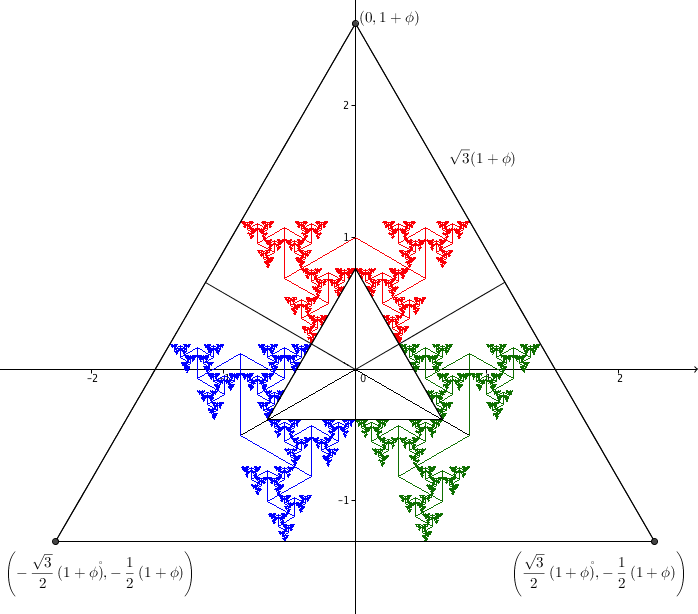
Point C is the branch tip for the path (RL)∞ and therefore its x-coordinate is [Details] \[ x =\frac{r\sin(120^\circ)}{1-r^2} = \frac{r\sin(120^\circ)}{r} = \sin(120^\circ) = \frac{\sqrt{3}}{2}. \] Therefore the length of segment BC is \(\sqrt{3}\). Since ABC is an equilateral triangle, we have \(h = \frac{\sqrt{3}}{2}\sqrt{3} = \frac{3}{2}\). The y-coordinate of the branch tip C is equal to [Details] \[ y = \frac{1+r\cos(120^\circ)}{1-r^2} = \frac{1+r\cos(120^\circ)}{r} = \frac{1}{r} - \frac{1}{2} = \phi - \frac{1}{2}. \] Hence the length of segment AD is \(R = \phi - \frac{1}{2} + \frac{3}{2} = \phi + 1\). This segment is the radius of the triangle's circumscribed circle, and therefore the length of the side of the triangle is equal to \(s = \sqrt{3}R = \sqrt{3}(\phi + 1).\)
Let \(\alpha = e^{120^\circ i}\). This complex number represents a counterclockwise rotation of 120°. The complex number \(\alpha^{-1}\) represents to a clockwise rotate of 120°.
Using that \(1-r^2 = r\), we can see that the branch tip for the path R2(LR)∞ in the red tree corresponds to the complex number \[ \begin{align} i + ir\alpha^{-1} + ir^2 \alpha^{-2} &+ ir^3 \alpha^{-1} + ir^4 \alpha^{-2} + ir^5 \alpha^{-1} + ir^6 \alpha^{-2} + ir^7 \alpha^{-1} + \cdots \\ \\ &= i + \frac{ir \alpha^{-1}}{1-r^2} + \frac{ir^2 \alpha^{-2}}{1-r^2} \\ \\ &= i + i\alpha^{-1} + ir\alpha^{-2} \end{align} \] Similarly, the branch tip for the path L2(RL)∞ in the red tree corresponds to the complex number \[ \begin{align} i + ir\alpha + ir^2 \alpha^2 &+ ir^3 \alpha + ir^4 \alpha^2 + ir^5 \alpha + ir^6 \alpha^2 + ir^7 \alpha + \cdots \\ \\ &= i +\frac{ir \alpha}{1-r^2} + \frac{ir^2 \alpha^2}{1-r^2} \\ \\ &= i + i\alpha + ir\alpha^2 \end{align} \] Rotating this last branch tip point by 120° clockwise corresponds to multiplying the complex number for the branch tip by \(\alpha^{-1}\). This means the rotated point becomes \(i\alpha^{-1} + i + ir\alpha\). But \(\alpha^3 = 1\) and therefore \(\alpha = \alpha^{-2}\). Therefore the rotated branch tip corresponds to the branch tip R2(LR)∞. Since the red golden tree is rotated by 120° clockwise to get the green golden tree, this shows that the red golden tree and the green golden tree just touch at this common branch point.
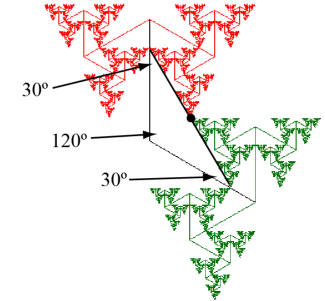The top edge of the red subtree whose trunk is the last branch of the path RR makes an angle of 30° with the main trunk [Proof]. The same is true of the top edge of the green subtree whose trunk is the last branch of the path LL. These two edges both contain the same point as shown above. Because the two trunks make an angle of 120°, and the sum of those three angles is 180°, the red and green edges must form a straight line segment (angle of 180°) since the sum of the interior angles of a quadrilateral is 360°.
By symmetry, the same thing happens for the green and blue trees, and for the blue and red trees. In particular, this means the edges of the three trees form an equilateral triangle around which the trees lie.
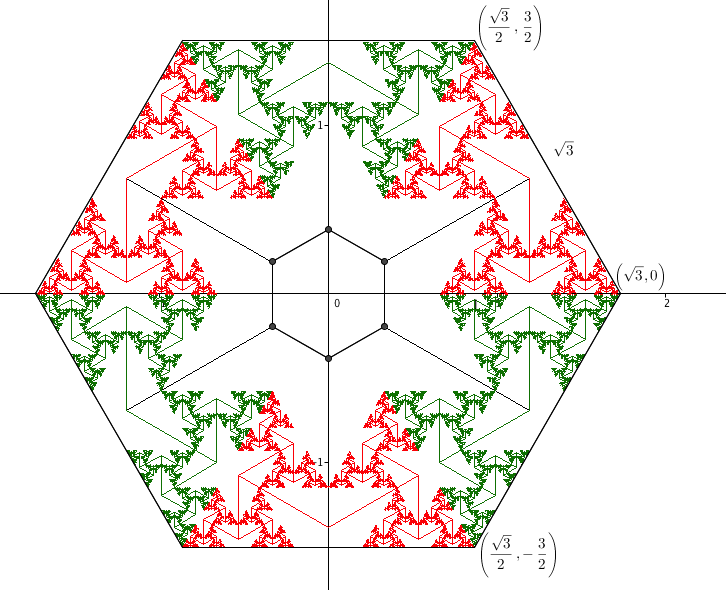
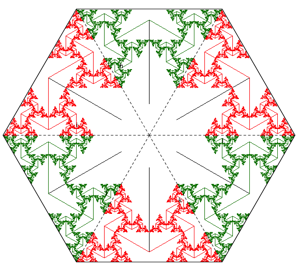The diagonals of a hexagon divides the hexagon into 6 equilateral triangles since the interior angles are 120°. The side edges of a golden 120° tree make an angle of 60° with the top edge of the tree [Proof]. If the trunk of the tree is of length 1, then the top edge is of length \(\sqrt{3}\). Therefore a golden 120° tree can be placed to fit exactly inside one of the equilateral triangles formed by the diagonals of a hexagon with sides of length \(\sqrt{3}\). Each of the other five equilateral triangles will also hold a golden 120° tree, and the side edges of the trees will touch along the diagonals of the hexagon.
The six trunks of the trees lie at the vertices of a hexagon with sides of length \(2-\phi\).
