Details about Golden 60° Symmetric Binary Trees

The three trees are placed so that their trunks start at the origin and are of length 1. The scaling factor is \(r = r_{sc} = \frac{1}{\phi}\) where \(\phi\) is the golden ratio. It is useful to note that \[ \phi^2 = \phi+1 \Rightarrow 1 = \frac{1}{\phi} + \frac{1}{\phi^2} \Rightarrow 1-\frac{1}{\phi^2} = \frac{1}{\phi} \Rightarrow 1-r^2 = r. \]

Side Length of Equilateral Triangle

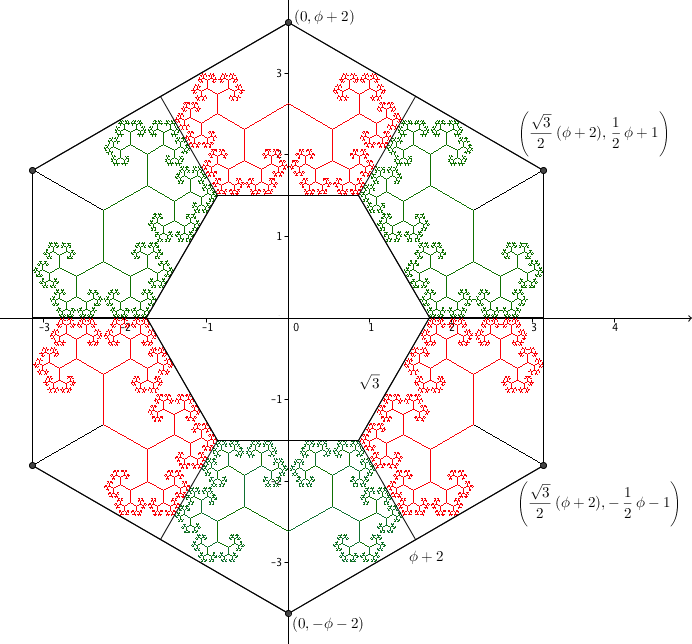
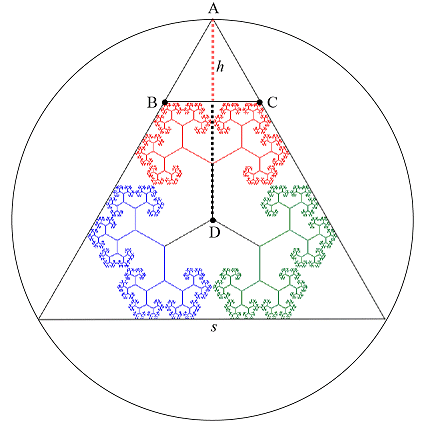
Point C is the branch tip for the path (RL)^∞ and therefore its x-coordinate is [Details] \[ x =\frac{r\sin(60^\circ)}{1-r^2} = \frac{r\sin(60^\circ)}{r} = \sin(60^\circ) = \frac{\sqrt{3}}{2}. \] Therefore the length of segment BC is \(\sqrt{3}\). Since ABC is an equilateral triangle, we have \(h = \frac{\sqrt{3}}{2}\sqrt{3} = \frac{3}{2}\). The y-coordinate of the branch tip C is equal to [Details] \[ y = \frac{1+r\cos(60^\circ)}{1-r^2} = \frac{1+r\cos(60^\circ)}{r} = \frac{1}{r} + \frac{1}{2} = \phi + \frac{1}{2}. \] Hence the length of segment AD is \(R = \phi + \frac{1}{2} + \frac{3}{2} = \phi + 2\). This segment is the radius of the triangle's circumscribed circle, and therefore the length of the side of the triangle is equal to \(\sqrt{3}R = \sqrt{3}(\phi + 2).\)

Intersection Points

Let \(\alpha = e^{60^\circ i}\). This complex number represents a counterclockwise rotation of 60°. The complex number \(\alpha^{-1}\) represents to a clockwise rotate of 60°.

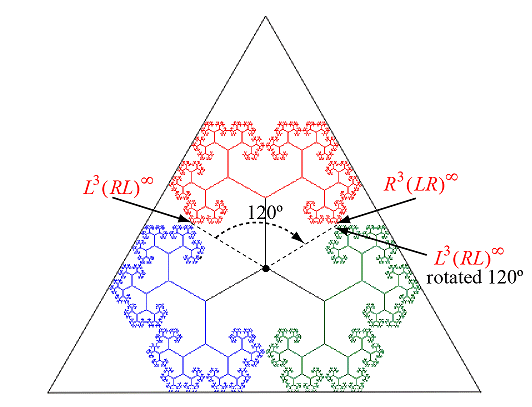
Using that \(1-r^2 = r\), we can see that the branch tip for the path R³(LR)^∞ in the red tree corresponds to the complex number \[ \begin{align} i + ir\alpha^{-1} + ir^2 \alpha^{-2} &+ ir^3 \alpha^{-3} + ir^4 \alpha^{-2} + ir^5 \alpha^{-3} + ir^6 \alpha^{-2} + ir^7 \alpha^{-3} + \cdots \\ \\ &= i + ir\alpha^{-1} + \frac{ir^2 \alpha^{-2}}{1-r^2} + \frac{ir^3 \alpha^{-3}}{1-r^2} \\ \\ &= i + ir\alpha^{-1} + ir\alpha^{-2} + ir^2\alpha^{-3} \\ \\ &= i + ir\alpha^{-1} + ir\alpha^{-2} - ir^2 \\ \\ &= ir + ir\alpha^{-1} + ir\alpha^{-2} = \frac{3}{\phi} + \frac{1}{\phi} i \end{align} \] (since \(\alpha^{-3} = -1\).) Similarly, the branch tip for the path L³(RL)^∞ in the red tree corresponds to the complex number \[ \begin{align} i + ir\alpha + ir^2 \alpha^2 &+ ir^3 \alpha^3 + ir^4 \alpha^2 + ir^5 \alpha^3 + ir^6 \alpha^2 + ir^7 \alpha^3 + \cdots \\ \\ &= i + ir\alpha + \frac{ir^2 \alpha^2}{1-r^2} + \frac{ir^3 \alpha^3}{1-r^2} \\ \\ &= i + ir\alpha + ir\alpha^2 + ir^2\alpha^3 \\ \\ &= i + ir\alpha + ir\alpha^2 - ir^2 \\ \\ &= ir + ir\alpha + ir\alpha^2 \end{align} \] (since \(\alpha^{3} = -1\).) Rotating this last branch tip point by 120° clockwise corresponds to multiplying the complex number for the branch tip by \(\alpha^{-2}\). This means the rotated point becomes \(ir\alpha^{-2} + ir\alpha^{-1} + ir\), which corresponds to the branch tip R³(LR)^∞. Since the red golden tree is rotated by 120° clockwise to get the green golden tree, this shows that the red golden tree and the green golden tree just touch at this common branch point. By symmetry, the same thing happens for the green and blue trees, and for the blue and red trees.

We claim that if the 6 copies of the golden 60° tree are placed around a regular hexagon with sides of length \(2+\phi\), then in the figure below the branch tip of the path (RL)^∞ for the green tree will coincide with the branch tip of the path (LR)^∞ for the red tree. For the sake of the computation we take the origin to be at the base of the trunk of the green tree.

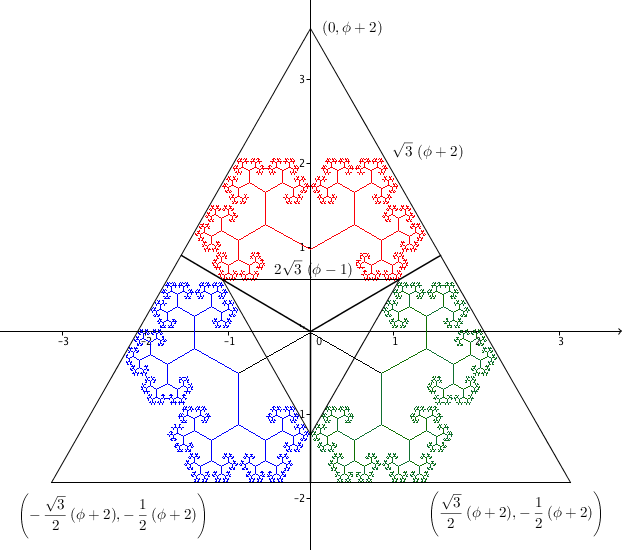
The trunk of the green tree can be taken to be the complex number i. The the branch tip for the green (RL)^∞ path corresponds to the complex number \[ \begin{align} i &+ ir\alpha^{-1} + ir^2 + ir\alpha^{-1} + ir^4 + ir^5\alpha^{-1} + \cdots \\ \\ &= \frac{i}{1-r^2} + \frac{ir\alpha^{-1}}{1-r^2} \\ \\ &= \frac{i}{r} + i \alpha^{-1}= i\phi + i \alpha^{-1} \\ \\ &= i\phi + i\left(\cos(60^\circ) - i\sin(60^\circ)\right) = \frac{\sqrt{3}}{2} + i\left(\phi+\frac{1}{2}\right) \end{align} \] The trunk of the red tree can be represented by the vector (as a complex number) \[k = -\cos(30^\circ) + i\sin(30^\circ) = -\frac{\sqrt{3}}{2} + \frac{1}{2}i.\] The vector S from the trunk of the green tree to the trunk of the red tree is given (as a complex number) by \[ S = (2+\phi)\left(\cos(30^\circ) + i\sin(30^\circ)\right) = (2+\phi)\left(\frac{\sqrt{3}}{2} + \frac{1}{2}i\right) \] The branch point for the red path (LR)^∞ is therefore \[ \begin{align} S &+ k + kr\alpha + kr^2 + kr^3\alpha + kr^4 + kr^5\alpha + \cdots \\ \\ &= S + \frac{k}{1-r^2} + \frac{kr\alpha}{1-r^2} \\ \\ &= S + k\phi + k\alpha \\ \\ &= (2+\phi)\left(\frac{\sqrt{3}}{2} + \frac{1}{2}i\right) + \left(-\frac{\sqrt{3}}{2}\phi + \frac{1}{2}\phi i\right) + \left(-\frac{\sqrt{3}}{2}+\frac{1}{2}i\right)\left(\frac{1}{2} + \frac{\sqrt{3}}{2}i\right) \\ \\ &= \sqrt{3} + i + \frac{\sqrt{3}}{2}\phi + \frac{1}{2}\phi i - \frac{\sqrt{3}}{2}\phi + \frac{1}{2}\phi i - \frac{\sqrt{3}}{2} - \frac{1}{2}i \\ \\ &= \frac{\sqrt{3}}{2} + i\left(\phi + \frac{1}{2}\right). \end{align} \] So the two branch tips are the same and the claim is verified. A similar set of calculations will show that the branch tip at R(RL)^∞ for the green tree will coincide with the branch tip at L(LR)^∞ for the red tree, with both equal to \[ \frac{\sqrt{3}}{2}\phi + i\left(2-\frac{1}{2}\phi\right). \] This means, in particular, that all the branch tips along the top of the green subtree that starts with the branch R trunk will coincide with the corresponding branch tips along the top of the red subtree that starts with the branch L trunk. The two trees fit together with no overlap.

By symmetry the same thing will happen with all the other golden 60° trees placed around the hexagon.