The Golden Self-Contracting Angles
The
golden ratio is
\[
\phi = \frac{1+\sqrt{5}}{2}.
\]
It is the unique positive solution to the equation \(x^2-x-1=0\), and its reciprocal \(1/\phi\) is the unique positive solution to \(x^2+x-1=0\). Two useful properties of \(\phi\) are that
\[
\begin{align}
\frac{1}{\phi} &= \phi-1 \\
\frac{1}{\phi^2} &= 2-\phi
\end{align}
\]
See the
Wikipedia article for more information.
Below is the graph of the self-contacting scaling factor as a function of θ, along with the horizontal line at \(1/\phi = 0.61803\ldots\). We see that there are exactly four intersections. We claim that these occur at θ = 60°, 108°, 120°, and 144°.
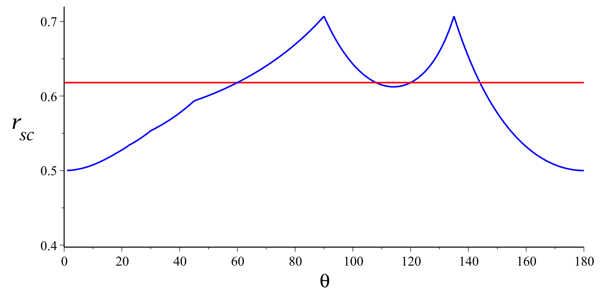
θ = 60°
When 0° < θ < 90°, the self-contacting scaling factor r is the unique solution [
Proof] to the equation
\[\sum_{k=0}^{N-1} r^{k+2}\cos(k\theta) = \frac{1}{2}\]
where N is the smallest integer such that Nθ ≥ 90°. If θ = 60°, then N = 2, and the equation for r is
\[
\frac{1}{2} = r^2 + r^3\cos(60^\circ) = r^2 + \frac{r^3}{2} \\ \\
\Rightarrow 0 = r^3 + 2r^2 - 1 = (r^2 + r - 1)(r+1)
\]
Therefore r satisfies \(r^2+r-1=0\), and hence \(r = 1/\phi\).
θ = 108°
For 90° < θ < 135°, the self-contacting factor r satisfies the equation [
Proof]
\[
(*) \quad 2\cos(2\theta)r^2 + 2\cos(\theta)r + 1 = 0
\]
If θ = 108°, then
\[
\begin{align}
\cos(108^\circ) &= \frac{1-\sqrt{5}}{4} = -\frac{1}{2\phi} = -\frac{1}{2}(\phi-1) \\ \\
\cos(216^\circ) &= 2\cos^2(108^\circ) - 1 = \frac{1}{2\phi^2}-1 = -\frac{\phi}{2}
\end{align}
\]
Substituting these into (*)
\[
2\cos(2\theta)r^2 + 2\cos(\theta)r + 1 = -\phi r^2 - (\phi-1)r + 1 = -(\phi r - 1)(r+1) = 0
\]
Therefore \(r_{sc} = 1/\phi\) is the solution when θ = 108°.
θ = 120°
We can still use (*) with θ = 120°. This gives
\[
\begin{align}
2\cos(2\theta)r^2 + 2\cos(\theta)r + 1 &= 2\cos(240^\circ)r^2 + 2\cos(120^\circ)r + 1 \\ \\
&= -r^2 - r + 1 = r^2+r-1
\end{align}
\]
and so \(r_{sc} = 1/\phi\) is the solution when θ = 120°.
θ = 144°
For 135° < θ < 180°, the self-contacting value is [
Proof]
\[r_{sc} = -\frac{1}{2\cos(\theta)}\]
Therefore when θ = 144°, we have
\[
r_{sc} = -\frac{1}{2\cos(144^\circ)} = -\frac{1}{-2\cos(36^\circ)} = \frac{1}{2\frac{1+\sqrt{5}}{4}} = \frac{2}{1+\sqrt{5}} = \frac{1}{\phi}.
\]



