Taylor series for \(f_\theta (r)\) near r = 0 (for top part of tree)

Recall that \(f_\theta (r) = y_k - y_0\) where y₀ is the y-coordinate of the branch tip for the path (LR)^∞ and y_k is the y-coordinate of the branch tip for the path R^k(LR)^∞, where k is the smallest integer such that kθ ≥ 360°. Note that k ≥ 3.

Let \(\alpha = e^{\theta i}\). The branch tip for R^k(LR)^∞ occurs at the point corresponding to the complex number \[ z_k = \left(i+ir\alpha^{-1} + ir^2\alpha^{-2} + ir^3\alpha^{-3} + \ldots + ir^k\alpha^{-k} \right)+ \left(ir^{k+1}\alpha^{-k+1} + ir^{k+2}\alpha^{-k} + \ldots\right). \] Then \[ \begin{align} y_k = \text{Im}(z_k) = 1 &+ r\cos(\theta) + r^2\cos(2\theta) + r^3\cos(3\theta) + \ldots \\ \\ &+ r^k\cos(k\theta) + r^{k+1}\cos((k-1)\theta) + r^{k+2}\cos(k\theta) + \ldots. \end{align} \] The branch tip for (LR)^∞ occurs at the point corresponding to the complex number \[ z_0 = i + ir\alpha + ir^2 + ir^3\alpha + ir^4 + ir^5\alpha + \ldots. \] Therefore \[ y_0 = \text{Im}(z_0) = 1 + r\cos(\theta) + r^2 + r^3\cos(\theta) + r^4 + r^5\cos(\theta) + \ldots. \] Subtracting the two expressions for the y-coordinates shows that \[ f_\theta (r) = (\cos(2\theta)-1)r^2 + (\cos(3\theta) - \cos(\theta))r^3 + \ldots. \]

When r is close to 0, the first r² term will dominate this expression. Therefore \(f_\theta (r)\) will behave like the quadratic function (cos(2θ)-1)r² when r is small. Since 0° < θ < 180°, the coefficient cos(2θ)-1 will be negative. Thus the graph of \(f_\theta (r)\) will be decreasing and concave down for small values of r.

Examples

Asking about the behavior of a function near r = 0 is really asking about the Taylor series for the function centered at r = 0. A computer algebra system like Maple or Mathematica can calculate a Taylor series up to a given order.

Example 1: θ = 60° (so k = 6)

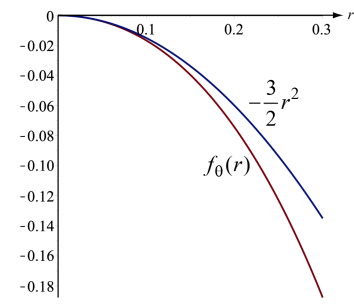\[ f_\theta (r) = -\frac{3}{2}r^2 -\frac{3}{2}r^3 -\frac{3}{2}r^4+ \ldots \]

Example 2: θ = 80° (so k = 5)

\[ f_\theta (r) = -1.93969r^2 - 0.67365r^3 - 0.23396r^4 + \dots \]