


The Hausdorff distance between two compact sets A and B is given by
\[D(A,B) = \inf \left\{ {r:A \subseteq {N_r}(B) \text{ and } B \subseteq {N_r}(A)} \right\}\]
where for a set W, Nr(W) is the r-envelope of W; that is, the set of all points that are within a distance r of some point in W.
Let T(0) be the initial square (shown in red in the figure below) and let T(1) be the first iteration (which adds the two gray squares to the initial red square). Let \(\alpha\) be the angle for the left square.
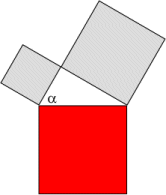
We want to determine the distance between T(0) and T(1). Since T(0) is a subset of T(1), then T(0) is also a subset of the r-envelope of T(1) for all values of r. Therefore we only need to look at the values of r for which T(1) is a subset of the r-envelope of T(0).
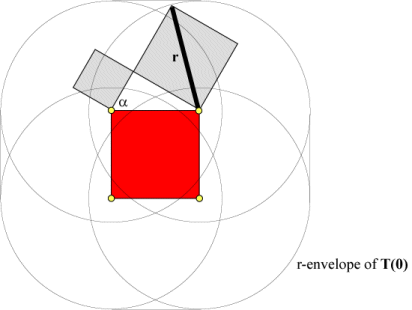
From this drawing we can see that the critical value of r is at most the length of the diagonal of the larger square that is added to T(0) to construct T(1). Let's assume that each side of T(0) has length 1. Then the sides of the two gray squares in T(1) have lengths \(\cos(\alpha)\) and \(\sin(\alpha)\). Let w be the larger of these lengths. Then
\[D \left( {T(0),T(1)} \right) \leqslant \sqrt 2 \cdot w\]What about the distance between T(1) and T(2)? Here we have the following situation

where the gray squares are added to T(1) (red region) to form T(2). As before, the critical value of r is at most the length of the diagonal of the larger gray square. The side of this gray square has length \({w^2}\) and therefore
\[D\left( {T(1),T(2)} \right) \leqslant \sqrt 2 \cdot {w^2}\]
Now the same idea can also be used to compute the distance between T(k) and T(k+1). This will be determined by the length of the diagonal of the larger square that is added to T(k) to get T(k+1). The side of the larger square has length \({w^{k+1}}\). Therefore
\[D\left( {T(k),T(k+1)} \right) \leqslant \sqrt 2 \cdot {w^{k+1}}\]
We actually want to show that the sequence of sets is a Cauchy sequence in the Hausdorff metric, so we need to get an estimate for the distance between T(n) and T(m) for m > n. But this is easy because the terms for the distance between consecutive sets are part of a geometric sequence with \(w < 1\).
\[\begin{aligned} D\left( {T(n),T(m)} \right) &\leqslant \sum\limits_{k = n}^{m - 1} {D\left( {T(k),T(k + 1)} \right)} \leqslant \sum\limits_{k = n}^\infty {D\left( {T(k),T(k + 1)} \right)} \\ &\leqslant \sum\limits_{k = n}^\infty {\sqrt 2 \cdot {w^{k + 1}}} = \frac{{\sqrt 2 \cdot {w^{n + 1}}}}{{1 - w}} \\ \end{aligned} \]
(The first inequality follows from using the triangle inequality for the Hausdorff metric.) Given a value for ε, all we need to do is pick N so that
\[\frac{{\sqrt 2 \cdot {w^{N + 1}}}}{{1 - w}} < \varepsilon \]
and then D(T(n), T(m)) < ε for all n, m > N. This shows that the sequence of sets is a Cauchy sequence in the Hausdorff metric and that the sets therefore converge to a limit.