λ < 1/2

If λ < 1/2, then the scaled triangles do not touch or overlap. The attractor is a self-similar fractal of dimension log(1/3)/log(λ).

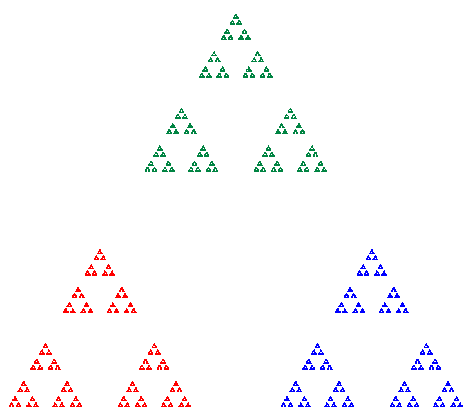
λ = 0.4

λ ≥ 2/3

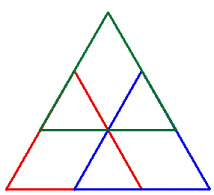The figure to the right shows the first iteration when λ = 2/3. The three scaled triangles exactly fit together to fill the original equilateral triangle with no holes. Thus the union of the three (filled) triangles coincides with the original (filled) triangle and the attractor for the IFS will be that original (filled) triangle. If λ > 2/3, then the scaled triangles will overlap even more and the attractor will still be the original (filled) triangle.
 

λ = 2/3

1/2 < λ < 2/3

Broomhead, Montaldi, and Sidorov showed that for this interval there is a countable family of values of λ for which the attractor of the IFS is what they call "total self-similar". These λ values are the multinacci numbers w_m, m ≥ 2, that are the unique positive solutions to the equations \[{x^m} + {x^{m - 1}} + \cdots + {x^2} + x = 1.\]

The first multinacci number w₂ is the solution to \({x^2} + x = 1\), so \({w_2} = \dfrac{{\sqrt 5 - 1}}{2} = 0.618034\) is the reciprocal of the golden ratio. The figure below shows the attractor of the IFS for λ = w₂.

λ = w₂ = 0.618034

In this image, the black region is \({f_2}({f_1}({f_1}({S_{{w_2}}})))\) where \(S_{w_2}\) is the fat Sierpinski gasket for λ = w₂. The green region is \({f_3}({f_2}({f_1}({S_{{w_2}}})))\). In both cases, notice that the holes for the black and green regions line up with the holes in the attractor. To see why this might happen, consider the following illustration showing the first iteration with λ = w₂.

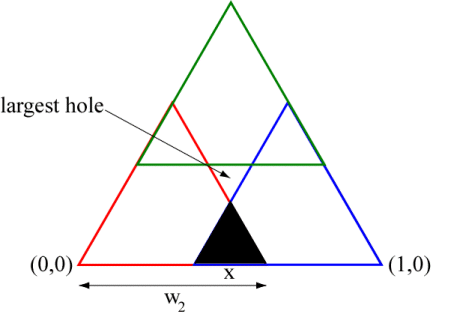
Observe that \(x = {w_2} - (1 - {w_2}) = 2{w_2} - 1\). Now \({w_2}^2 + {w_2} = 1\) and therefore

\[{w_2}^3 = {w_2} - {w_2}^2 = {w_2} - (1 - {w_2}) = 2{w_2} - 1 = x\]

Notice also that the lower left vertex of the black triangle is at the same point as the blue triangle. What this all means is that if the original triangle is scaled three times by the factor w₂ and translated to (1−w₂,0), it will be in the same location as the black triangle. The same thing would happen in applying f₁, f₁, and f₂ in succession to the attractor \(S_{w_2}\). A similar analysis can be done for the green triangle (which has also been scaled by w₂ three times.)

The second multinacci number, w₃, is the solution to \({x^3} + {x^2} + x = 1\), so

\[{w_3} = \frac{1}{3}{\left( {17 + 3\sqrt {33} } \right)^{1/3}} - \frac{2}{{3{{\left( {17 + 3\sqrt {33} } \right)}^{1/3}}}} - \frac{1}{3} = 0.543689\]

The attractor for λ = w₃ is shown below.

λ = w₃ = 0.543689

Notice that it looks more like the Sierpinski gasket because w₃ is closer to 1/2 than w₂ is. (In fact, the multinacci numbers w_m converge to 1/2 as m goes to infinity since in the limit, the left side of the equation satisfied by the multinacci numbers becomes a geometric series with sum \(\frac{x}{1-x}\) and that equation has the solution x = 1/2.) The attractor for w₃ has the same total self-similarity property as for w₂.

In this case the original triangle can been scaled by w₃ four times and then translated to produce the black triangle where the red and blue triangles overlap. This is because \(x = {w_3} - (1 - {w_3}) = 2{w_3} - 1\) and \({w_3}^3 +{w_2}^2 + {w_2} = 1\) so that

\[{w_3}^4 = {w_3} - {w_3}^2 - {w_3}^3 = {w_3} - {w_3}^2 - (1 - {w_3} - {w_3}^2) = 2{w_3} - 1 = x\]