


|
\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{1/2} & 0 \\
0 & {1/2} \\
\end{array}} \right]{\bf{x}}\) |
scale by 1/2 |
|
\({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{1/2} & 0 \\
0 & {1/2} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{1/2} \\
0 \\
\end{array}} \right]\) |
scale by 1/2 |
| \({f_3}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} {1/2} & 0 \\ 0 & {1/2} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {1/4} \\ {\sqrt{3}/4} \\ \end{array}} \right]\) | scale by 1/2 |
If the elements in the \(Z_3\) cyclic group \(\{r_0, r_{120}, r_{240}\}\) consisting of rotations by \(0^\circ\), \(120^\circ\), and \(240^\circ\), respectively, are composed with the functions in the Sierpinski IFS, then the resulting IFS will have the following 9 functions, all of which involve a scaling by 1/2 and the following rotations.
|
\({h_1}({\bf{x}}) = {r_0}\,{f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{1/2} & 0 \\
0 & {1/2} \\
\end{array}} \right]{\bf{x}}\) |
no rotation |
|
\({h_2}({\bf{x}}) = {r_{120}}\,{f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{-1/4} & -\sqrt{3}/4 \\
\sqrt{3}/4 & {-1/4} \\
\end{array}} \right]{\bf{x}}\) |
rotate by \(120^\circ\) |
|
\({h_3}({\bf{x}}) = {r_{240}}\,{f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{-1/4} & \sqrt{3}/4 \\
-\sqrt{3}/4 & {-1/4} \\
\end{array}} \right]{\bf{x}}\) |
rotate by \(240^\circ\) |
|
\({h_4}({\bf{x}}) = {r_0}\,{f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{1/2} & 0 \\
0 & {1/2} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{1/2} \\
0 \\
\end{array}} \right]\) |
no rotation |
|
\({h_5}({\bf{x}}) = {r_{120}}\,{f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{-1/4} & -\sqrt{3}/4 \\
\sqrt{3}/4 & {-1/4} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{-1/4} \\
\sqrt{3}/4 \\
\end{array}} \right]\) |
rotate by \(120^\circ\) |
|
\({h_6}({\bf{x}}) = {r_{240}}\,{f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{-1/4} & \sqrt{3}/4 \\
-\sqrt{3}/4 & {-1/4} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{-1/4} \\
-\sqrt{3}/4 \\
\end{array}} \right]\) |
rotate by \(240^\circ\) |
|
\({h_7}({\bf{x}}) = {r_0}\,{f_3}\,({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{1/2} & 0 \\
0 & {1/2} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{1/4} \\
\sqrt{3}/4 \\
\end{array}} \right]\) |
no rotation |
|
\({h_8}({\bf{x}}) = {r_{120}}\,{f_3}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{-1/4} & -\sqrt{3}/4 \\
\sqrt{3}/4 & {-1/4} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{-1/2} \\
0 \\
\end{array}} \right]\) |
rotate by \(120^\circ\) |
|
\({h_9}({\bf{x}}) = {r_{240}}\,{f_3}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{-1/4} & \sqrt{3}/4 \\
-\sqrt{3}/4 & {-1/4} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{1/4} \\
-\sqrt{3}/4 \\
\end{array}} \right]\) |
rotate by \(240^\circ\) |

Here is an image of the Z3 Sierpinski triangle drawn with pixel coloring. The overlapping of the nine scaled images shown above contributes to how some pixels are hit much more often than others when the fractal is drawn using the random algorithm.
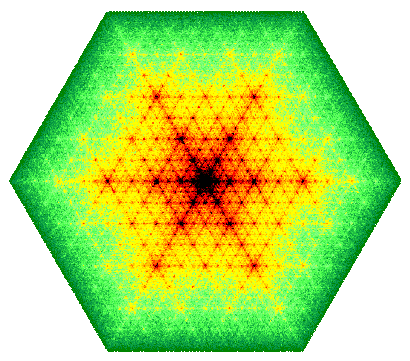
More details about symmetric fractals can be found here.