

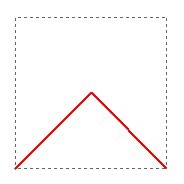
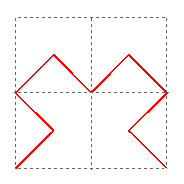
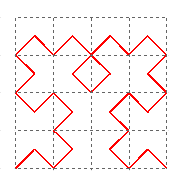
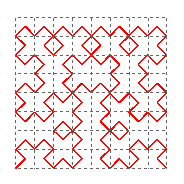
Construction
Animation
Each iteration will produce a continuous polygonal path that starts at the lower left corner of the original square and ends at the lower right corner. This path will intersect but never cross itself. The limit of this sequence of continuous paths will produce a continuous Peano space-filling curve that passes through every point in the original square. In other words, the limit set of this iterative construction will be the filled square. You can get a sense of why this should happen since the nth iteration produces a continuous polygonal path consisting of 4n pairs of triangular line segments with each pair lying in a square of edge length 1/2n. As those squares shrink in size as n goes to infinity, the polygonal path will cover more and more of the initial square. Given any particular point in the square, one can make the polygonal path go arbitrarily close to that point by taking the nth iteration for a sufficient large n. [For a more formal proof, see the topology text by Munkres.]
IFS
Animation
|
\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
0 & {1/2} \\
{-1/2} & 0 \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
0 \\
{1/2} \\
\end{array}} \right]\) |
scale by 1/2, rotate −90° |
|
\({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{1/2} & 0 \\
0 & {1/2} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{0} \\
{1/2} \\
\end{array}} \right]\) |
scale by 1/2 |
|
\({f_3}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{1/2} & 0 \\
0 & {1/2} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{1/2} \\
{1/2} \\
\end{array}} \right]\) |
scale by 1/2 |
| \({f_4}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} 0 & {-1/2} \\ {1/2} & 0 \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {1} \\ 0 \\ \end{array}} \right]\) | scale by 1/2, rotate 90° |
The attractor for this IFS is the filled-in unit square [0,1]x[0,1] with four self-similar parts (the four subsquares.) The black "L" in each colored square indicates the orientation of that square according to the corresponding function in the IFS.
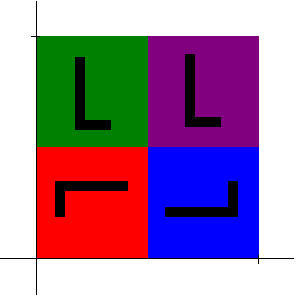
$$\sum\limits_{k = 1}^4 {{r^d}} = 1\quad \Rightarrow \quad d = \frac{{\log (1/4)}}{{\log (r)}} = \frac{{2\log (1/2)}}{{\log (1/2)}} = 2$$

[Enlarge]
Space Filling Curve (6th Iteration)
12.5" x 12.5" (14 point canvas)
Larry Riddle, 2013