Rotating a Fractal
Let \(\{ f_i : i = 1,2,\dots,n \}\) be an IFS where each affine transformation \(f_i : R^2 \to R^2\) is of the form \(f_i (x) = \lambda_i M_ix + b_i\) with \(0 < \lambda_i < 1\), \(M_i\) a rotation matrix, and \(b_i\) a translation vector. Let \(R\) be a (counterclockwise) rotation matrix through an angle \(\beta\) and let \(\alpha > 0\). Form a new IFS consisting of the functions \(g_i (x) = \lambda_i M_ix + \alpha Rb_i\). In other words, the linear part of each transformation in the new IFS has not changed, but each translation vector in the original IFS has been rotated counterclockwise through the angle \(\beta\) and scaled by the factor \(\alpha\).Let \(A\) be the unique attractor for the IFS \(\{ f_i : i = 1,2,\dots,n \}\). We claim that \(\alpha R(A)\) is the attractor for the IFS \(\{ g_i : i = 1,2,\dots,n \}\). First we note that \[A = \bigcup_{i=1}^{n} f_i(A) = \bigcup_{i=1}^{n} \left( \lambda_i M_i(A) + b_i \right)\] Since rotation matrices commute, we get that \[ \begin{align} \alpha R(A) &= \alpha R\left( \bigcup_{i=1}^{n} \left( \lambda_i M_i(A) + b_i \right) \right) \\ \\ &= \bigcup_{i=1}^{n} \left( \alpha \lambda_i RM_i(A) + \alpha Rb_i \right) \\ \\ &= \bigcup_{i=1}^{n} \left( \lambda_i M_i \left( \alpha R(A) \right) + \alpha Rb_i \right) \\ \\ &= \bigcup_{i=1}^{n} g_i \left( \alpha R(A) \right) \end{align} \]
This shows that \(\alpha R(A)\) is the fixed point for the \(\{g_i\}\) IFS and thus is the attractor for that IFS.
For example, if we take the IFS for the Sierpinski gasket
\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} {1/2} & 0 \\ 0 & {1/2} \\ \end{array}} \right]{\bf{x}}\)
\({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} {1/2} & 0 \\ 0 & {1/2} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {1/2} \\ 0 \\ \end{array}} \right]\)
\({f_3}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} {1/2} & 0 \\ 0 & {1/2} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {1/4} \\ {\sqrt{3}/4} \\ \end{array}} \right]\)
and we want to rotate that through an angle of 135° counterclockwise and scale by \(\frac{1}{\sqrt 2}\), the new translation vectors would be
\(\frac{1}{{\sqrt 2 }}\left[ {\begin{array}{*{20}{c}} { - \frac{{\sqrt 2 }}{2}}&{ - \frac{{\sqrt 2 }}{2}}\\ {\frac{{\sqrt 2 }}{2}}&{ - \frac{{\sqrt 2 }}{2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 0\\ 0 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0\\ 0 \end{array}} \right]\)
\(\frac{1}{{\sqrt 2 }}\left[ {\begin{array}{*{20}{c}} { - \frac{{\sqrt 2 }}{2}}&{ - \frac{{\sqrt 2 }}{2}}\\ {\frac{{\sqrt 2 }}{2}}&{ - \frac{{\sqrt 2 }}{2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {1/2}\\ 0 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \frac{1}{4}}\\ {\frac{1}{4}} \end{array}} \right]\)
\(\frac{1}{{\sqrt 2 }}\left[ {\begin{array}{*{20}{c}} { - \frac{{\sqrt 2 }}{2}}&{ - \frac{{\sqrt 2 }}{2}}\\ {\frac{{\sqrt 2 }}{2}}&{ - \frac{{\sqrt 2 }}{2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {1/4}\\ {\sqrt 3 /4} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \frac{1}{8} - \frac{{\sqrt 3 }}{8}}\\ {\frac{1}{8} - \frac{{\sqrt 3 }}{8}} \end{array}} \right]\)
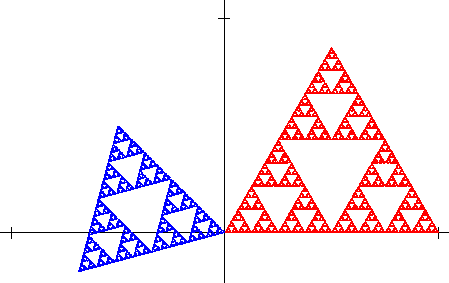
The figure below shows the original Sierpinski gasket in red and the attractor for the new IFS in blue after the rotation and scaling.