 How to Create a Fractal Tiling Design
How to Create a Fractal Tiling Design
- Select Design\Examples\Tiling with Integer Matrices
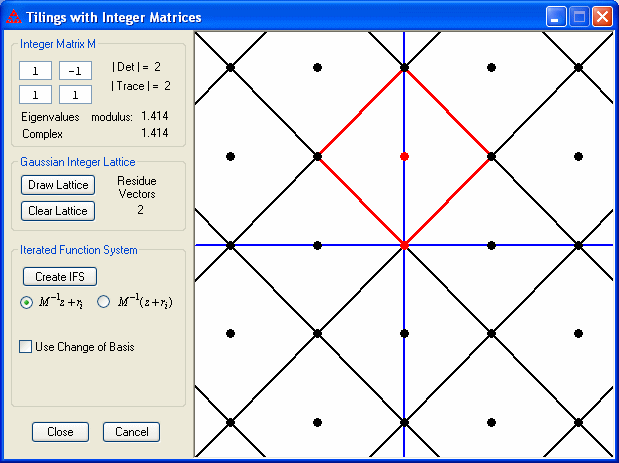
- Construct the integer matrix M. Both eigenvalues should have modulus larger than 1. For example, you can take M = [1 -1 ; 1 1] (first and second rows) as shown in the figure below.
- Click on "Draw Lattice". You can change the window view using the keyboard keys
- Page Up - zoom in
- Page Down - zoom out
- Arrow keys - shift left, right, up, or down
- Home - default view
- Choose m = | det(M) | residue vectors by clicking on the dots. These dots consist of points with integer coefficients. In the figure below, one point has been chosen at the origin and the second point directly above. Notice that both points are on or inside the red parallelogram (containing the principal residue vectors). The other parallelograms contain points that are considered members of the same residue class. The program will not allow you to choose two points from the same residue class. Clicking on a red dot will remove it from the residue system. You might try, for example, to remove the point at (0,1) and choose the point (1,0) instead, which is a member of the same residue class as (0,1).
- Click on "Create IFS" when done.
- The two options under the "Create IFS" button create the IFS using different algorithms. You can try both options to see the effect.
- It is possible to choose a change of basis matrix B to construct tiles with radial symmetry (if m = 2, 3, 4, 5, or 7.) Check "Use Change of Basis" and enter the values for B. Then click on "Draw Lattice" and choose (or change) the residue vectors.
- You can copy the lattice image to the clipboard with the standard Copy menu command (or type ctrl-C), or you can click in the picture box with the right mouse button to get a contextual menu with options to copy the image or save it to a file in gif, png, jpeg, or bitmap format.

For more details, see the articles
"Fractal Tilings in the Plane," Richard Darst, Judith Palagallo, and Thomas Price, Mathematics Magazine, Vol. 71, No. 1, February 1998, 12-23. [JSTOR (subscription required)]
"Analyzing the Area of Fractal Tilings," Miyuki Breen and Judith Palagallo, The Pi Mu Epsilon Journal, Vol. 11, No. 8, Spring 2003, 413-422.
The file tilings.ifs contains some of the examples from these papers (particularly the first).

