 How to Tile
How to Tile

- Create an IFS that will tile the plane. This can be done, for example, using the Fractal Tiling with Integer Matrices design.
- Choose Tiling Options from the Draw menu. This window must be open to draw the tiling.
- The tiling is done by translating the IFS fractal in the direction of the vector nv+kw where v and w are vectors you specify, and n and k are integers between -R and R, where R is the tiling radius. This produces (2R+1)2 copies of the original fractal.
- If the IFS is based on the design using integer matrices, the vectors v and w are initially set to be the same as the columns of the integer matrix. This will work in many cases, but it may be necessary to make adjustments.
-
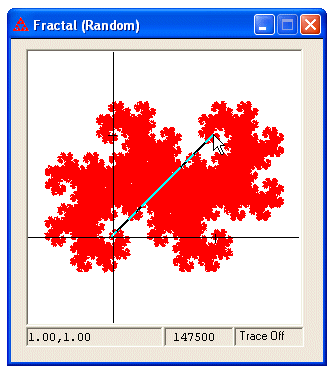
It is sometimes helpful to measure distances in the Fractal window to know how to choose the vectors v and w. This can be done by pressing the left mouse button while holding down the ctrl key. Continue to press the button and move the cursor to another location. The message box in the lower left corner will display the change in x and the change in y between the two points. The line connecting the two points and the Δx and Δy values will disappear when you release the mouse button. The image below illustrates an attempt to measure how the point at the origin should be shifted to place a new tile. Notice in this case that the shift matches the vector v shown in the tiling options figure above.
- Choose the tiling radius. The larger the value, the more tiles will be produces but the longer it will take. If you pick 0 for the tiling radius, only the original fractal will be drawn.
- There are two possible coloring schemes. The first will use the IFS colors on each copy as specified for the functions in the IFS window. The second scheme will color the entire tile based on the colors in the Tiling Options dialog. These nine colors are repeated as needed. You can click on any of the boxes to change the color used.
- Once all choices have been made, draw the tiles using either the random method or the deterministic method.
Here is a tiling with tiling radius 3.



