How to Create a Fractal derived from a Complex Base

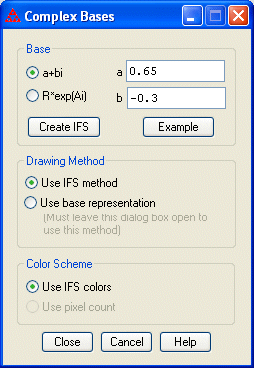
  1. Select Design\Examples\Fractals derived from a Complex Base
  2. Choose a complex number z with |z| < 1 to use as the base. This can be done in the form a+bi or in the form ReAi. Click on the Example button to cycle through various examples.
  3. Click on "Create IFS".
  4. Choose a drawing method. You can use either the random or deterministic IFS methods, or you can draw the image based on the base representation. The latter method will compute and plot points of the form Σ zn for n in A, where A is a subset of the integers {1, 2, ..., 22}. If you want to use this method to draw the image, you must leave the dialog box open when you do the drawing.
  5. Choose a coloring method. If using the IFS drawing method your only choice is to use the IFS coloring methods. If you use the drawing method based on the base representation, you can choose to use a solid color or to color each pixel based on the number of times the pixel is plotted as one of the finite sums.
  6. To see the location of z in the fractal image, turn on Trace and set the initial point to z. If you continue to press 2, you can trace out the path of the points z, z2+z, z3+z2+z, etc. It is helpful to set the color of the points to black.

For more details, see the articles:

"Number Systems With a Complex Base: A Fractal Tool for Teaching Topology," Daniel Goffinet, American Mathematical Monthly, Vol. 98, No. 3 (March 1991), 249-255. [JSTOR (subscription required)]

"Fractal Tilings Derived from Complex Bases," Sara Hagey and Judith Palagallo, The Mathematical Gazette, Vol. 85, No. 503 (July 2001), 194-201. [JSTOR (subscription required)]

Following are some values of complex numbers used in the first article. You can load these from the complex.ifs file downloaded with the program.

  1. z = 0.65 − 0.3i
  2. z = 0.8 + 0.2i
  3. z = −0.697e2πi/5
  4. z = −0.62e2πi/7
  5. z = 0.9(−cos(π/13) + sin(π/13)i)