How to Create Sierpinski Triangle Designs

Select Design\Examples\Sierpinski Triangle

The standard Sierpinski triangle consists of picking the midpoints along the three sides of a triangle and removing the triangle formed from those midpoints. This design dialog box allows you to pick other points a, b, and c along the three sides rather than just the midpoints. The points may be entered as a factor of the length of the respective side. The factors are measured in a counter-clockwise direction. So the factor for point a equals |Ba|/|BC|, the factor for point b equals |Cb|/|CA|, and the factor for point c equals |Ac|/|AB|. You can also use the mouse to move the points along the sides. A third option is to click on the Random button and have the program pick three points at random. You can also move vertex A with the mouse by clicking on the small circle at vertex A. Vertex A is restricted to remain with the unit square (with side AB as the base of the unit square). Click on the Default button to restore vertex A and the three midpoints to the standard Sierpinski equilateral triangle.

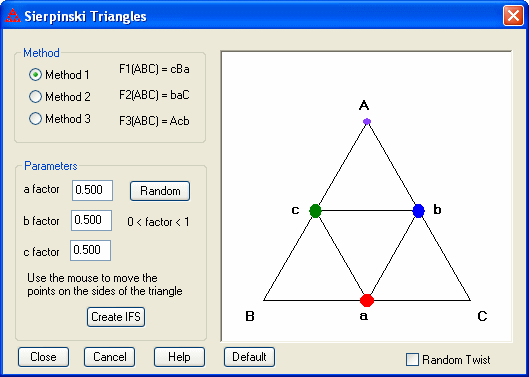
dialog box

Rather than constructing the Sierpinski triangle by removing interior triangles, you can view the construction as transforming the large triangle ABC into each of three smaller triangles by mapping each vertex of ABC to a vertex of the smaller triangle.

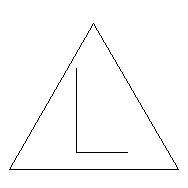
polygon method 1 design method 1 fractal

Method 1 is the same as removing the interior triangle since the orientation of the vertices is not changed. The functions in the IFS map the vertices of triangle ABC in the following way (see the labeling in the window above): 

F1(ABC) = cBa
F2(ABC) = baC
F3(ABC) = Acb
So map F1 maps vertex A of the large triangle to vertex c of the small triangle, vertex B to vertex B, and vertex C to vertex a.

polygon method 2 design method 2 fractal

Method 2 maps one vertex to itself, but switches the orientation of the other two vertices. The functions in the IFS map the vertices of triangle ABC in the following way (see the labeling in the window above): 

F1(ABC) = aBc
F2(ABC) = abC
F3(ABC) = Abc

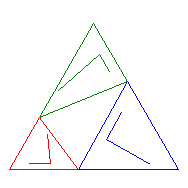
polygon method 3 design method 3 fractal

Method 3 keeps the same orientation for the vertices in the larger and smaller triangles, but reverses the direction. The functions in the IFS map the vertices of triangle ABC in the following way (see the labeling in the window above): 

F1(ABC) = caB
F2(ABC) = Cab
F3(ABC) = cAb

Once you have chosen the method and parameters, click on the "Create IFS" button to create the IFS in the IFS window. The program will, be default, use an oriented triangle to illustrate the design (as shown in the examples above).