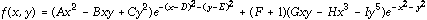 .
.In [1], Sheldon Gordon described several investigations that he has calculus students perform on polynomials whose coefficients are determined by the digits of the students' social security numbers. He remarks that the use of individualized projects are designed to get the students to take a personal interest in the topic under study and that the students seem to enjoy these types of investigations. In this note I would like to build upon this theme by describing a project that I have used in multivariable calculus classes.
The goal of the project is to investigate a function of two variables built from the student's social security number. First the student is asked to take each of the nine digits of the number and compute its value mod 3 (to keep the digits small). Writing the new number as ABC-DE-FGHI, the student constructs a function by substituting the digits into the expression
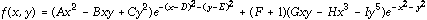 .
.
The exponential terms guarantee that the function is very close to 0 outside a circle of relatively small radius. Thus a student with the social security number 123-45-6789, for example, would substitute the digits of 120-12-0120 to get the individualized function
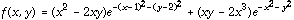 .
.
Now the student must investigate this function to give a general description of
what the surface looks like, determine the number and approximate locations of
all local maximas, minimas and saddle points, and find the location and value
of the absolute maximum and the absolute minimum. Moreover, the student is
asked to compute the maximum and minimum values of the function along the circle
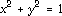 .
.
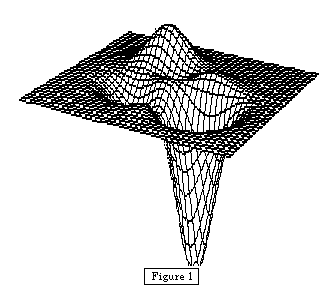 Students are used to max-min problems that have nice closed-form solutions
that are easily computed. This is a non-trivial function to analyze, however,
that requires a proper mix of theory to know where to look and software tools
to provide the computational assistance. We use
MPP3D
[2] to draw the surface
(see Figure 1),
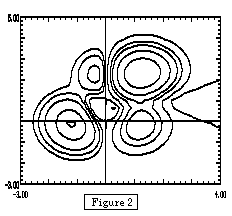
MDEP
[3] to draw level curves (see Figure 2), and
Derive
[4] to
compute values of the function, to compute partial derivatives, and to find
approximate solutions, using Newton's method, to the nonlinear systems of
equations that arise in the investigations. The student's ability to interpret
the behavior of the level curves is important to help spot possible critical
points. Estimates of the locations of the critical points may then be used as
initial guesses in Derive's utility file for Newton's method when solving for
the zeros of the gradient. I like to use MDEP because it allows the students to
selectively choose which level curves to plot. This is important for regions
such as the one just above the origin in Figure 2. There are several clues that
something interesting is happening there. First, the origin is a saddle point
(the function f is constructed so that the origin will be a critical
point), and second, the function takes the value 0 along the y-axis.
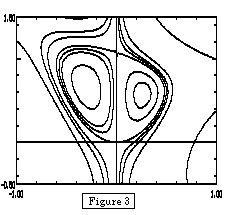
Figure 3 shows the results of investigating the behavior of the function in the
smaller region [-1, 1] by [-0.5, 1.5]. The values along the level curves range
between -0.5 and 0.1, and reveal another relative min, relative max, and saddle
point.
Students are used to max-min problems that have nice closed-form solutions
that are easily computed. This is a non-trivial function to analyze, however,
that requires a proper mix of theory to know where to look and software tools
to provide the computational assistance. We use
MPP3D
[2] to draw the surface
(see Figure 1),
MDEP
[3] to draw level curves (see Figure 2), and
Derive
[4] to
compute values of the function, to compute partial derivatives, and to find
approximate solutions, using Newton's method, to the nonlinear systems of
equations that arise in the investigations. The student's ability to interpret
the behavior of the level curves is important to help spot possible critical
points. Estimates of the locations of the critical points may then be used as
initial guesses in Derive's utility file for Newton's method when solving for
the zeros of the gradient. I like to use MDEP because it allows the students to
selectively choose which level curves to plot. This is important for regions
such as the one just above the origin in Figure 2. There are several clues that
something interesting is happening there. First, the origin is a saddle point
(the function f is constructed so that the origin will be a critical
point), and second, the function takes the value 0 along the y-axis.
Figure 3 shows the results of investigating the behavior of the function in the
smaller region [-1, 1] by [-0.5, 1.5]. The values along the level curves range
between -0.5 and 0.1, and reveal another relative min, relative max, and saddle
point.
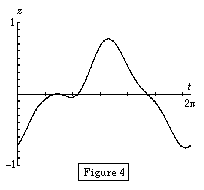
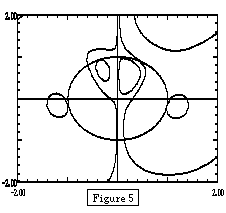
There are two methods a student could choose to investigate the maximum and minimum values of the function along the unit circle. The first would be to parametrize the circle as x=cos(t), y=sin(t) and then plot z=f(x,y)=f(cos(t),sin(t)) as a function of t (see Figure 4). This is how the theory of Lagrange multipliers is often explained, although the constraint curve is not usually so easily parametrized. Alternatively, combining this theory with the practical difficulties of solving the three nonlinear equations that arise from the use of Lagrange multipliers provides an interesting illustration of the geometric interpretation of constrained optimization. The student could search for where the level curves of f are approximately tangent to the constraint curve to find good initial estimates to use in Newton's method. Figure 5 shows the four level curves that correspond to the four critical values in Figure 4.
An integral part of this investigation is the student's written project report. I stress that the student knows much more about her function than I do and that it is therefore her responsibility to accurately summarize the methods and results of the investigation if I am to understand the behavior of her function. In addition, because each student has a different function to consider, I encourage collaboration and discussion among groups of students, which I believe contributes to the learning experience. My students enjoy these assignments more than traditional homework problems because of their individual nature and because of the interesting phenomena that can occur. It is not unusual for a student to proudly show off her surface and describe its features. Finally, I even enjoy grading these types of assignments because I become as much an investigator as the students.
The programs MPP 3D and MDEP are available from the Mathematics Archive at the University of Tennessee at Knoxville.
Last modified: April 14, 1996