

$$ B(0) \supset B(1) \supset B(2) \supset B(3) \supset \cdots $$
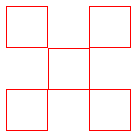
The box fractal is the intersection of all the sets in this sequence, that is, the set of points that remain after this construction is repeated infinitely often. The figures below show the first three iterations.

|

|

|

|
|||
| B(0) | B(1) | B(2) | B(3) |
\[ \begin{align} f_1 ({\bf{x}}) &= \left[ {\begin{array}{*{20}c} {1/3} & 0 \\ 0 & {1/3} \\ \end{array}} \right]{\bf{x}} \\ f_2 ({\bf{x}}) &= \left[ {\begin{array}{*{20}c} {1/3} & 0 \\ 0 & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}c} 0 \\ {2/3} \\ \end{array}} \right] \\ f_3 ({\bf{x}}) &= \left[ {\begin{array}{*{20}c} {1/3} & 0 \\ 0 & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}c} {1/3} \\ {1/3} \\ \end{array}} \right] \\ f_4 ({\bf{x}}) &= \left[ {\begin{array}{*{20}c} {1/3} & 0 \\ 0 & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}c} {2/3} \\ 0 \\ \end{array}} \right] \\ f_5 ({\bf{x}}) &= \left[ {\begin{array}{*{20}c} {1/3} & 0 \\ 0 & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}c} {2/3} \\ {2/3} \\ \end{array}} \right] \\ \end{align} \]
The box fractal consists of 5 self-similar pieces corresponding to the five functions in the iterated function system.
This will produce the outline of the box fractal.

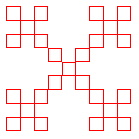
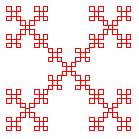
$$\sum\limits_{k = 1}^5 {{r^d}} = 1\quad \Rightarrow \quad d = \frac{{\log (1/5)}}{{\log (r)}} = \frac{{\log (1/5)}}{{\log (1/3)}} = \frac{{\log (5)}}{{\log (3)}} = 1.46497$$
The box fractal is one example of a fractal antenna that is used in cell phones to maximize reception in a minimum amount of space.
