

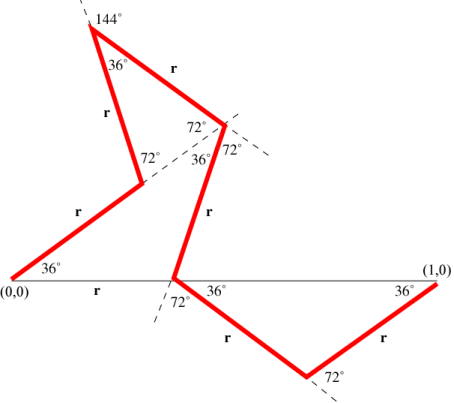
The six red line segments in the figure give the basic motif (first iteration) for this IFS. Each subsequent iteration is done by replacing each line segment with a scaled version of the basic motif.
These six transformations are given by rotations of 36°, 108°, -36°, -108°, -36°, and 36° respectively. Thus the endpoints of the fourth segment and the last segment lie on the x-axis. The value of r must be chosen so that the endpoint of the last segment is at the point (1,0). From the figure we see that we must have
\[\begin{array}{l} r + 2r\cos {36^ \circ } = 1 \\ \Rightarrow r = \frac{1}{{1 + 2\cos {{36}^ \circ }}} = \frac{1}{{1 + 2\left( {\frac{{1 + \sqrt 5 }}{4}} \right)}} = \frac{{3 - \sqrt 5 }}{2} = 0.381966 \\ \end{array}\]
|
\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{0.309} & { - 0.255} \\
{0.255} & {0.309} \\
\end{array}} \right]{\bf{x}}\)
|
scale by r, rotate by 36° |
|
\({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ - 0.118} & { - 0.363} \\
{0.363} & { - 0.118} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{0.309} \\
{0.225} \\
\end{array}} \right]\)
|
scale by r, rotate by 108° |
|
\({f_3}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{0.309} & {0.225} \\
{ - 0.225} & {0.309} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{0.191} \\
{0.588} \\
\end{array}} \right]\)
|
scale by r, rotate by −36° |
|
\({f_4}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ - 0.118} & {0.363} \\
{ - 0.363} & { - 0.118} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{0.500} \\
{0.363} \\
\end{array}} \right]\)
|
scale by r, rotate by −108° |
|
\({f_5}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{0.309} & {0.225} \\
{ - 0.225} & {0.309} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{0.382} \\
0 \\
\end{array}} \right]\)
|
scale by r, rotate by −36° |
| \({f_6}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} {0.309} & { - 0.225} \\ {0.225} & {0.309} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {0.691} \\ { - 0.225} \\ \end{array}} \right]\) | scale by r, rotate by 36° |

First three iterations of the L-system
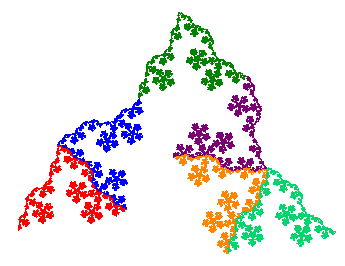
Four iterations
\[\sum\limits_{k = 1}^6 {{r^d}} = 1 \quad \Rightarrow \quad d = \frac{{\log (1/6)}}{{\log (r )}} = 1.86172\]

William A. McWorter was born on July 15, 1932 and died in
Delaware, Ohio on October 22, 2009. He received his Ph.D in mathematics from The Ohio State University in 1963 with a dissertation in an area of group theory, and eventually became an associate professor of mathematics at Ohio State. The pentigree was discovered by accident during his hunts for "dragons", a category of fractals and
space-filling curves that McWorter described as "organism[s] of cells
arranged according to a genetic code." The most complete analysis of
the pentigree can be found in the text by Gerald Edgar.
Photo Source: OSU Department of Mathematics Newsletter, Summer 2021