Iterated Function
Systems
Larry Riddle
Home Sierpinski Gasket Sierpinski Carpet Sierpinski Pentagon Heighway Dragon
McWorter Pentigree Pentadentrite Koch Curve Koch Snowflake Levy Dragon

Pentadentrite

The pentadentrite is a variation of the McWorter's pentigree. Starting from the origin, draw a line segment of length r at an angle A. Turn left by 72° and draw another line segment of length r. Next turn right by 72° and draw a third line segment of length r. The remaining three line segments, each of length r, are formed by making a right turn of 144° followed by two left turns of 72°. The end of the last line segment will be at the point (1,0).


Animation
(16Kb)

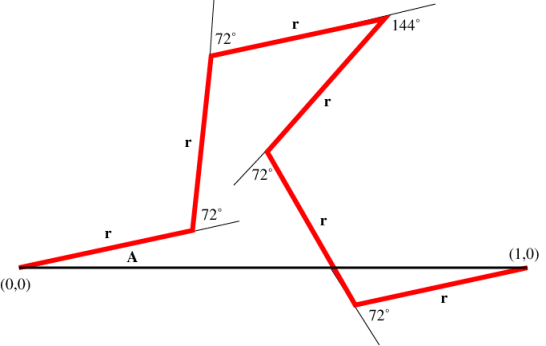
If A0 is the line segment from the origin to the point (1,0), then the six red line segments in the figure give the first iteration A1 for this construction. The scaling factor r and the angle A must be chosen so that the endpoint of the last segment is at the point (1,0).

The following calculations show that and A = 11.8186°.

It is now possible to determine how each of the six rotated segments must be translated. For example, the first segment must be scaled by r and rotated through the angle A. The second segment is rotated through an angle of A + 72°, scaled by r, then translated to (r sin A°, r sin A°). Similar calculations with the other segments led to the following IFS:

Angle 72
Axiom F
Generator F --> F+F-F- -F+F+F
(this will be rotated from the IFS constructed curve)


First three iterations of the L-system

We have a hyperbolic IFS with each map being a similitude of ratio r < 1. Therefore the similarity dimension, d, of the unique invariant set of the IFS is the solution to

This is called a pentadentrite because five copies of the limit set fit perfectly together to form the following shape:

 
  1. Edgar, Gerald A. Measure, Topology, and Fractal Geometry, Springer-Verlag, 1990.
Home Sierpinski Gasket Sierpinski Carpet Sierpinski Pentagon Heighway Dragon
McWorter Pentigree Pentadentrite Koch Curve Koch Snowflake Levy Dragon