


The boundary of the terdragon is the union of two self-similar pieces. The red piece is the top boundary and the blue piece (a rotation of the red piece by 180°) is the bottom boundary.


Put them together by clicking on the buttons to the left in sequence

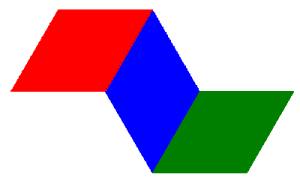
The figure on the left below shows the first level in the construction of the terdragon. The figure to the right shows a red envelope on top and a blue envelope on the bottom.
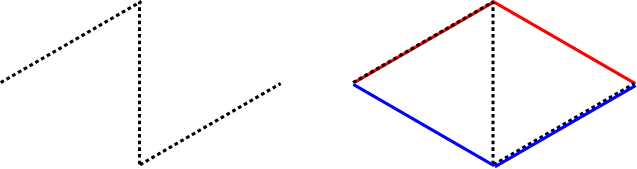
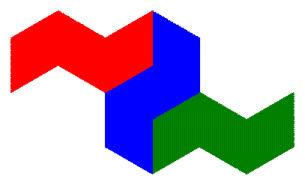
If we go to the next level (shown in the figure on the left below), we can connect endpoints of the line segments that form level 2 of the terdragon to form an envelope around the terdragon (red on top, blue on bottom).
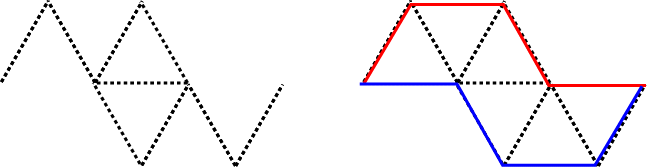
Below we show the same construction for level 3 and level 4.
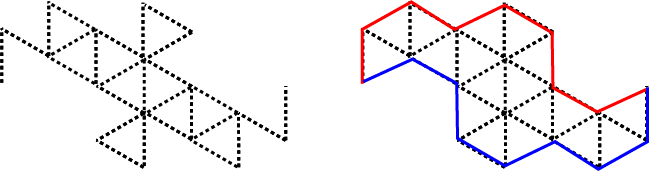
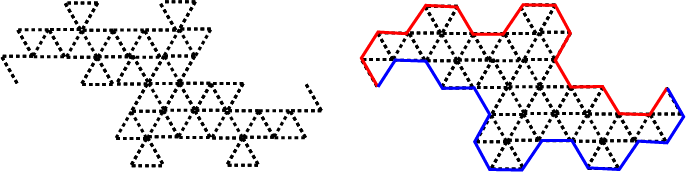
When this construction is continued ad infinitum, the red and blue envelopes will converge to the boundary of the terdragon.
These envelopes are also what we get if we apply the IFS for the terdragon starting with the level 1 parallelogram shown above. You can see in the figure below that the level 2 envelope consists of three copies of the level 1 parallelogram, two of which (red and green) have been rotated by 30° and one (blue) by −90° (clockwise rotation). In the same way, the level 3 envelope is obtained by applying the terdragon IFS to the level 2 envelope.
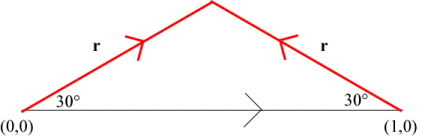
This yields the following IFS for the top boundary:
|
\({T_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{1/2} & { - \sqrt 3 /6} \\
{\sqrt 3 / 6} & {1/2} \\
\end{array}} \right]{\bf{x}} \) |
scale by \(\frac{1}{\sqrt 3}\), rotate by 30° |
|
\({T_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ - 1/2} & { - \sqrt 3 / 6} \\
{\sqrt 3 / 6} & { -1/2} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
1 \\
0 \\
\end{array}} \right]\) |
scale by \(\frac{1}{\sqrt 3}\), rotate by 150° |
The IFS for the bottom boundary is based on the following figure. Again, starting at the origin, each segment is replaced by a copy of the motif alternating between left and right.
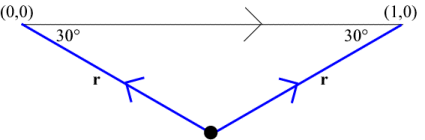
This gives the following IFS for the bottom boundary:
|
\({B_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ - 1/2} & { - \sqrt 3 / 6} \\
{\sqrt 3 / 6} & { -1/2} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
1/2 \\
-\sqrt 3 / 6 \\
\end{array}} \right]\) |
scale by \(\frac{1}{\sqrt 3}\), rotate by 150° |
|
\({B_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 1/2} & { - \sqrt 3 / 6} \\
{\sqrt 3 / 6} & { 1/2} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
1/2 \\
-\sqrt 3 / 6 \\
\end{array}} \right]\) |
scale by \(\frac{1}{\sqrt 3}\), rotate by 30° |
The axiom creates two segments going in opposite directions. This will then produce both the top and bottom boundaries at the same time.
\[\sum\limits_{k = 1}^2 {{r^d}} = 1 \quad \Rightarrow \quad d = \frac{{\log (1/2)}}{{\log (1/\sqrt 3 )}} = \frac{\log 4}{\log 3} = 1.26186\]