Representing the Terdragon Curve Symbolically

We consider the terdragon curve as constructed using line segments starting with an initial horizontal segment. Let \(T_n\) denote the \(n\)th iteration. It consists of \(3^n\) segments and \(3^n-1\) corners. To get the next iteration, \(T_{n+1}\), each of the segments in \(T_n\) is replaced by three segments, always starting the new segments to the left of the segment they replace from the previous iteration and in such a way that the new middle segment makes an angle of 60° with the first and third segments. Each iteration can be represented symbolically by a sequence consisting of the letters R and L. One can imagine moving along the individual segments making up the curve start at the left endpoint. A 60° corner is labeled R if the curve makes a right turn there, and is labeled L if the curve makes a left turn at that corner. The following image shows the symbolic coding for the first two iterations.

 
This construction can also be described by the following IFS:

\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} {1/2} & { - \sqrt 3 / 6} \\ {\sqrt 3 / 6} & {1/2} \\ \end{array}} \right]{\bf{x}}\)	scale by \(1/ \sqrt 3\), rotate by 30°
\({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} { 0} & { \sqrt 3 /3} \\ {-\sqrt 3 /3} & { 0} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} 1/2 \\ \sqrt 3 / 6 \\ \end{array}} \right]\)	scale by \(1/ \sqrt 3\), rotate by −90°
\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} {1/2} & { - \sqrt 3 / 6} \\ {\sqrt 3 / 6} & {1/2} \\ \end{array}} \right]{\bf{x}}+ \left[ {\begin{array}{*{20}{c}} 1/2 \\ -\sqrt 3 / 6 \\ \end{array}} \right]\)	scale by \(1/ \sqrt 3\), rotate by 30°

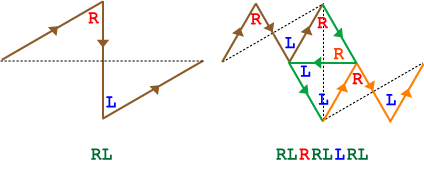
Notice that in the iterations for \(T_1\) and \(T_2\) shown above, the sequence for \(T_{2}\) consists of three copies of the sequence for \(T_1\) (shown in green) separated by R and L, respectively.

This recursive pattern holds for all iterations since \[T_{n+1} = f_1(T_n) \cup f_2(T_n) \cup f_3(T_n)\] as depicted in the following image:

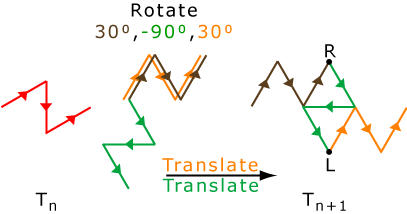
The first function in the iterated function system will just rotate \(T_n\) by 30° (which becomes the brown piece in the image above). This will not change the direction of the turn at each corner of \(T_n\), so the first part of \(T_{n+1}\) will have the same sequence of turns as \(T_n\). The second function in the IFS will rotate \(T_n\) by −90° (the green piece) and then translate so that the beginning of the green piece joins the end of the brown piece. The two pieces then form a new corner that has a right turn of 60°, so an R must be added to the end of the sequence from \(T_n\). The sequence of the turns in the second piece has not changed, however, so another copy of \(T_n\) follows that R. Finally, the third function will rotate \(T_n\) by 30° (which becomes the orange piece) and translates so that the beginning of the orange piece joins the end of the green piece. The second and third pieces form a new corner that has a left turn of 60°, so an L must be inserted. But again, the sequence of turns in the third piece has not changed so a final copy of \(T_n\) is added. (The IFS will also scale each piece, but this will not affect the direction of each turn.)

In their 1970 paper, Knuth and Davis expressed this relationship (with slightly different notation) as \(T_{n+1} = T_nRT_nLT_n\).

Since \(T_2\) = RLRRLLRL, we know that \(T_3\) must consist of three copies of this sequence separated by an R and L, respectively. So

\(T_3 = T_2RT_2LT_2\) = RLRRLLRL R RLRRLLRL L RLRRLLRL

The image below shows \(T_3\) with each segment colored either Red or bLue based on the sequence above. Following the curve starting at the black dot, each Red segment ends with a turn to the right, and each bLue segment ends with a turn to the left (the last segment is not part of the code, but is colored Red since in the next iteration there would be right turn at the end of this segment). Paying attention to the colors, can you trace the curve from end to end?

The curve can be traversed from the left endpoint to the right endpoint in such a way that the curve intersects only at corners and never crosses itself. [Demonstration with \(T_5\) and \(T_{7}\)]

Building the code for higher order iterations can be done recursively using the algorithm described above. Fortunately there is another method that can give the code for \(T_n\) directly. It is based on the following two observations.

Let the turns at the corners of \(T_n\) be denoted by \(a_i\) for \(1 \le i \le m\) and let the turns at the corners of \(T_{n+1}\) be denoted by \(b_i\) for \(1 \le i \le 3m+1\), where \(m=3^n-1\).

1. \(T_{n+1}\) is obtained by replacing each of the segments in \(T_n\) with three segments, always in the same orientation with a right turn between the first and second segments, and a left turn between the second and third segments. These are the corners in \(T_{n+1}\) that are in positions 1 and 2, 4 and 5, 7 and 8, etc., i.e the corners that are congruent to 1 and 2 mod 3. Therefore corner \(r\) has a right turn if \(r \text{ mod } 3 = 1\) and a left turn if \(r \text{ mod } 3 = 2\).
2. The corner corresponding to \(b_{3k}\) in iteration \(T_{n+1}\) coincides with the corner corresponding to \(a_k\) in \(T_n\). The following images show the two possible orientations for the segments in \(T_n\) and \(T_{n+1}\) at this common corner (the direction of the initial segment of \(T_n\) might be different, but this would not change the relative behavior of the other segments in the two figures.)

   

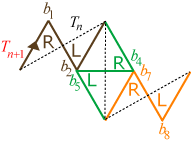
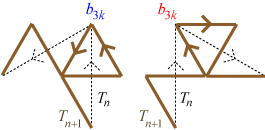
   In the left image, each curve turns to the left at the common corner. In the right image, each curve turns to the right at the common corner.Therefore \(b_{3k}=a_k\) for \(1 \le k \le m\). We know, however, that \(T_{n+1}\) begins with \(T_n\) and therefore \(b_k = a_k\) for \(1 \le i \le m\). This means that \(b_{3k} = b_k\) for \(1 \le k \le m\).

These two observations provide an algorithm for how to generate the symbolic code for \(T_n\). First write out as many pairs of RL as needed, leaving a gap between each pair. Then fill in the gap at position 3k with the value at position k. For example, here is how it could be done for \(T_3\). Since \(3^3-1=26\), there are 9 pairs of RL separated by 8 gaps. Fill gap 3 with the value in position 1: Fill gap 6 with the value in position 2: Fill gap 9 with the value in position 3: Fill gap 12 with the value in position 4: Fill gap 15 with the value in position 5: Fill gap 18 with the value in position 6: Fill gap 21 with the value in position 7: Fill gap 24 with the value in position 8:

This is a convenient method to do by hand for small values of \(n\). For larger iterations, however, it is not difficult to write a short program to generate the code using the two observations above. [Python example]

Try it!
Iteration number (1 to 8)
n = Compute code Clear

The final method gives a way to calculate directly whether the \(r\)th turn is R or L. Write \(r = k3^m\) where \(k\) is not a multiple of 3.

• If \(k \text{ mod } 3 = 1\), then turn right (R)
• If \(k \text{ mod } 3 = 2\), then turn left (L)

Here is why that works.

If \(r\) is not a multiple of 3, then \(k=r\) and \(m=0\). As shown above in method 2, the curve turns right if \(r \text { mod } 3 =1\) and turns left if \(r \text { mod } 3 = 2\).

If \(r\) is a multiple of 3, where \(r = k2^m\) and \(k\) is not a multiple of 3, then by the second observation in method 2, the direction of the turn at corner \(r\) is the same as the direction of the turn at corner \(k\) because you can keep dividing the corner number by 3 without changing the direction of the turn. But \(k\) is not a multiple of 3, so now the same argument as before applies to show that the direction of the turn at corner \(k\) is determined by the value of \(k \text{ mod } 3.\)

For example, in \(T_{10}\), which has 59048 corners, the direction at turn 4554 is L because \(4554=506 \cdot 3^2\) and \(506 \text{ mod } 3 = 2\).

The terdragon is equal to \(\displaystyle \lim_{n \rightarrow \infty} T_n\). Since each \(T_{n+1}\) begins with \(T_n\), it makes sense to express the terdragon as the infinite sequence of R's and L's obtained as each finite sequence for \(T_n\) is extended to the limit. Given any particular position in the infinite sequence, method 3 above can be used to determine whether the code in that position is R or L.

Try it!

Position r = Compute

 
 

1. Donald Knuth and Chandler Davis, "Number Representatives and Dragon Curves," Journal of Recreational Mathematics, Vol. 3 (1970), 66-81 and 133-149. Reprinted in Selected Papers on Fun and Game by Donald Knuth, Center for the Study of Language and Information, Stanford University, 2010, pp571-614.