
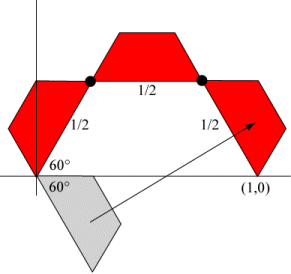
The first scaled trapezoid must be rotated by 60°. The second scaled trapezoid is just translated so that the point at the origin is moved to the point \((1/4,\sqrt 3 /4)\). The third scaled trapezoid is rotated by −60° and then translated so that the point at the origin moves to the point \((3/4,\sqrt 3 /4)\). This yields the following IFS.
|
\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{1/4} & { - \sqrt 3 /4} \\
{\sqrt 3 /4} & {1/4} \\
\end{array}} \right]{\bf{x}}\) |
scale by 1/2, rotate by 60° |
|
\({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 1/2} & { 0} \\
{ 0} & { 1/2} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
1/4 \\
\sqrt 3 /4 \\
\end{array}} \right]\) |
scale by 1/2 |
|
\({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{1/4} & { \sqrt 3 /4} \\
{- \sqrt 3 /4} & {1/4} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
3/4 \\
\sqrt 3 /4 \\
\end{array}} \right]\) |
scale by 1/2, rotate by −60° |
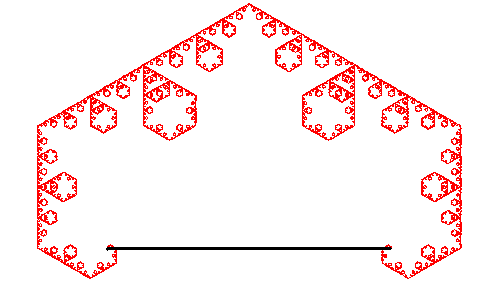
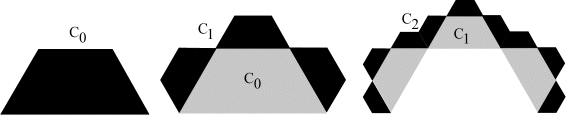
The Lévy diamonds consists of three self-similar pieces corresponding to the three functions in the iterated function system.
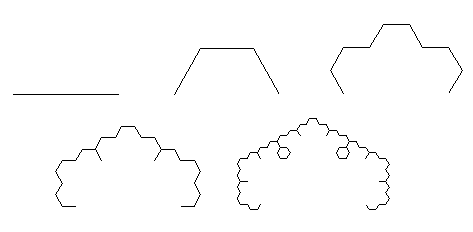
First four iterations of the L-system
8 iterations
\[\sum\limits_{k = 1}^3 {{r^d}} = 1 \quad \Rightarrow \quad d = \frac{{\log (1/3)}}{{\log (1/2 )}} = \frac{\log 3}{\log 2} = 1.58496\]