


|
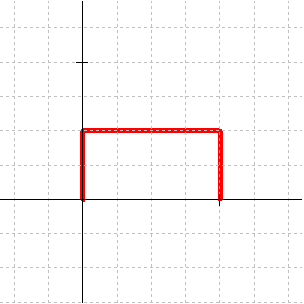
Start the construction of the Lévy dragon with a segment of length 1 along the x-axis. Two iterations produces the figure to the left that has a vertical segment along the y-axis. The left edge is at x = 0, the top edge at y = 0.5, the right edge at x = 1, and the bottom edge at y = 0. The grid size is 1/4 x 1/4. |

|
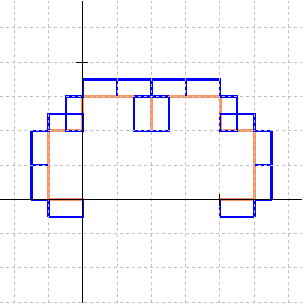
Each iteration produces either horizontal/vertical segments (even iteration) or segments at 45°/135° (odd iteration). The odd iterations will expand the size outward. The next even iteration will keep the size but make the segments vertical or horizontal. Here is the result after the 3rd iteration (green) and the 4th iteration (orange). The left (and by symmetry, the right) edge is extended by (1/2)2 = 1/4. The top edge has also expanded up by 1/4. The bottom edge is still at y = 0. |
|
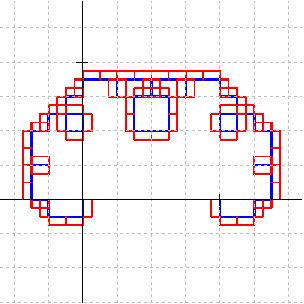
Because at iteration 4 there is a horizontal line segment along the x-axis, starting with the 5th iteration the dragon will begin to expand downwards. At iteration 6, each of the four edges will have been extended by an additional (1/2)3 = 1/8. |
|
At iteration 8, all four edges are extended by another (1/2)4 = 1/16. |
This pattern continues with the extension of the four edges by an additional (1/2)n at iteration 2n. The growth in the size of the Lévy dragon is therefore given by the following geometric series.
| Left/Right | \[{\left( {\frac{1}{2}} \right)^2} + {\left( {\frac{1}{2}} \right)^3} + {\left( {\frac{1}{2}} \right)^4} + \ldots = \frac{{\frac{1}{4}}}{{1 - \frac{1}{2}}} = \frac{{\frac{1}{4}}}{{\frac{1}{1}}} = \frac{1}{2}\] |
| Top | \[\left( {\frac{1}{2}} \right) + {\left( {\frac{1}{2}} \right)^2} + {\left( {\frac{1}{2}} \right)^3} + \ldots = \frac{{\frac{1}{2}}}{{1 - \frac{1}{2}}} = \frac{{\frac{1}{2}}}{{\frac{1}{2}}} = 1\] |
| Bottom | \[{\left( {\frac{1}{2}} \right)^3} + {\left( {\frac{1}{2}} \right)^4} + {\left( {\frac{1}{2}} \right)^5} + \ldots = \frac{{\frac{1}{8}}}{{1 - \frac{1}{2}}} = \frac{{\frac{1}{8}}}{{\frac{1}{2}}} = \frac{1}{4}\] |
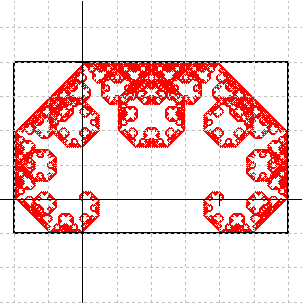
If you use the bounding rectangle as the initial set for the iteration, then each time the IFS is iterated the rectangles will continue to bound more but smaller copies of the dragon. Can you see the scaled copies in the images below as you click each button?
