Iterated Function
Systems
Larry Riddle

Home	Sierpinski Gasket	Sierpinski Carpet	Sierpinski Pentagon	Heighway Dragon
McWorter Pentigree	Pentadentrite	Koch Curve	Koch Snowflake	Levy Dragon

Tiling the Plane with the Lévy Dragon

L2 Tiling
Animation
(132Kb)

In his 1938 paper, Lévy wrote [see Edgar]

Moreover, it has the very curious property that, if [the dragon curve] were materialized, one could tile the plane with it, i.e., one can cover the plane with identical copies of this curve such that no two copies intersect, and such that no space is left uncovered.

Here is one way to visualize why this tiling works. The plane can certainly by tiled by unit squares. Divide each unit square into four congruent isoceles right triangles, each a congruent copy of L0, the isoceles right triangle with base along the unit interval and vertex at (1/2, 1/2). This was the triangle used in the description of of the construction of the Levy dragon. Applying the first step of the Lévy dragon construction to each of these triangles produces four congruent copies of L1 that still cover the unit square (see Figure 1).

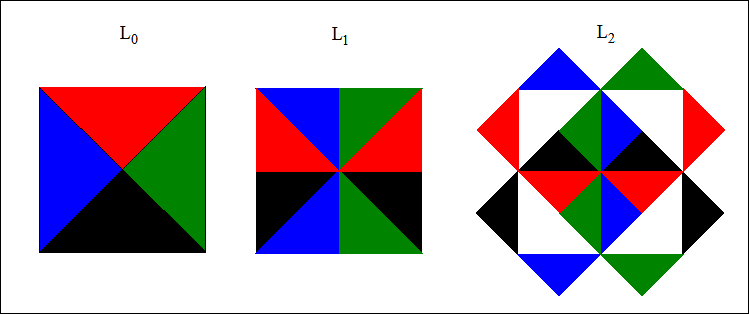
Figure 1

Now apply the next step of the construction to each of these regions. Some of the new triangles will now point outward, leaving what appears to be empty space in the square in Figure 1. But of course, we are also doing this construction to each of the surrounding unit squares, and as Figure 2 illustrates, some of the triangles from those surrounding squares produce new triangles that fill in the gaps.

Figure 2

Below in Figure 3 we see the tiling from the original unit square and the 8 surrounding unit squares. The gaps along the edges would be filled in by the congruent copies of L2 formed by iterating the triangles in the unit squares even further out.

Figure 3

The Quicktime animation illustrates how the eight surrounding copies fit with the center unit square to form the tiling. It is rather like connecting the pieces of a jigsaw puzzle. The entire plane can thus be tiled with congruent copies of L2.

Notice in the tilings using L2 that the unit square can be split into 4 smaller squares of area 1/4 that resemble the original pattern of four isoceles right triangles in the tiling with L0. We saw how the plane continues to be tiled in going from L0 to L1 to L2. Because the tiling for L2 consists of the same pattern as for L0, only on a smaller scale, the same construction would show that L3 and L4 continue to tile the plane. Here is a picture of congruent copies of L4 starting to tile the plane. Again, the gaps you see would be filled in from the copies generated by the unit squares further outside.

Tiling
Animation
(58Kb)

Now the tiling for L4 can again be split into squares of area 1/16 that resemble the original pattern of four isoceles right triangles, so we can proceed just as before. Continuing this way, an induction argument can then be used to show that congruent copies of Lk can tile the plane for every value of k. This result will therefore remain true for the limit set, and so Lévy's dragon will tile the plane. The Quicktime movie shows the progression of tilings for L0 through L6.

Reference: Lévy, P. "Plane or space curves and surfaces consisting of parts similar to the whole," in Classics on Fractals, Gerald A. Edgar, Editor, Addison-Wesley, 181-239.

Home	Sierpinski Gasket	Sierpinski Carpet	Sierpinski Pentagon	Heighway Dragon
McWorter Pentigree	Pentadentrite	Koch Curve	Koch Snowflake	Levy Dragon