Scale Factor and Translations for n-gons
Scale Factor
Suppose the initial polygon has n sides, each of length 1. The polygon must be scaled so that n copies of the scaled polygon exactly fit inside the initial polygon. The following figure illustrates one side of the initial polygon and two copies of the polygon after it is scaled by r and and the copies are translated.
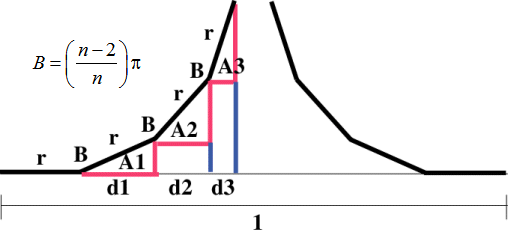
Two sides of the scaled polygons would eventually just meet at a vertex (except for when n is a multiple of 4, in which case the two polygons meet along an entire edge.) Notice that the sides of the polygon on the left form the hypotenuses of a sequence of right triangles, with each hypothenuse of length r. We need to determine the angles A1, A2, A3, etc. so that we can compute the lengths d1, d2, d3, etc. of the bases of each triangle.
The interior angle B of a regular n-sided polygon is (n-2)/n*pi. Working our way around the edges of the polygon, we get
\[\begin{array}{l} A1 = \pi - \frac{{n - 2}}{n}\pi = \frac{{2\pi }}{n} \\ A2 = 2\pi - B - \frac{\pi }{2} - \left( {\frac{\pi }{2} - A1} \right) = \frac{{2\pi }}{n} + A1 = \frac{{2\pi \cdot 2}}{n} \\ A3 = 2\pi - B - \frac{\pi }{2} - \left( {\frac{\pi }{2} - A2} \right) = \frac{{2\pi }}{n} + A2 = \frac{{2\pi \cdot 3}}{n} \\ \end{array}\]
There seems to be a pattern, and indeed, you can prove by induction that \(Ak = \frac{{2\pi \cdot k}}{n}\) for each angle Ak along the edges until the polygon meets the next polygon. We are ok in constructing these angles and corresponding triangles as long as the angle is still acute. This means we must have
\[Ak = \frac{{2\pi \cdot k}}{n} \le \frac{\pi }{2} \quad \Rightarrow \quad k \le \frac{n}{4}\]
Now that we know the angles, we can compute the lengths dk = r*cos(Ak) for k = 1 to \(\left\lfloor {n/4} \right\rfloor \). By symmetry, we have the same lengths for the polygon on the right. Therefore we have
\[{2 \; \left( {r + \sum\limits_{k = 1}^{\left\lfloor {n/4} \right\rfloor } {r \cos \left( {\frac{{2\pi k}}{n}} \right)} } \right)} = 1 \quad \Rightarrow \quad r = \frac{1}{{2 \; \left( {1 + \sum\limits_{k = 1}^{\left\lfloor {n/4} \right\rfloor } {\cos \left( {\frac{{2\pi k}}{n}} \right)} } \right)}}\]
Note that if n is a multiple of 4, then n/4 will be an integer. For that value of k, we have Ak = pi/2, so that the corresponding edge is vertical. In this case, the left and right polygons meet along this edge. See the figure.
Translations
Because the affine transformations for this iterated function system involve only scaling by r and translations, each vertex of the initial polygon is a fixed point for the transformation that translates the scaled version back to that vertex.

If we look at a particular vertex V for the corresponding transformation f(x)=r*x + b, then
\[V = f(V) = rV + b \Rightarrow b = (1 - r)V\]
So we just need to pick the vertices in a convenient way. The easiest way to do this is to place the initial polygon with its center at the origin and with one vertex on the x-axis.
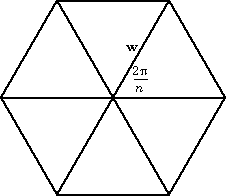
Each central angle is equal to 2*pi/n, so if w denotes the distance from the center to the vertex, then the vertices are at the points (w*cos(2 pi*k/n), w*sin(2 pi*k/n) for k = 1 to n. Therefore, the translation for the kth function is
\[(1 - r) \; \left[ {\begin{array}{*{20}{c}} {w \cdot \cos \left( {\frac{{2\pi k}}{n}} \right)} \\ {w \cdot \sin \left( {\frac{{2\pi k}}{n}} \right)} \\ \end{array}} \right]\]

