\(\lim_{r \rightarrow 1^{-}} f_\theta (r)\) when θ is a zero of N(θ)

Here we have N(θ) = 0 where \(\theta = \frac{540^\circ}{p}\) for p ≥ 4 or \(\theta = \frac{360^\circ}{2p+1}\) for p ≥ 1. \[ \begin{align} f_\theta (r) &= \sum_{n={k+1}}^{m}{r^n \sin(n \theta)} \\ \\ &+ \frac{r^{m+1} \sin((m-1)\theta) + r^{m+2} \sin(m \theta) - r^{k+1} \sin((k-1)\theta) - r^{k+2} \sin(k \theta)}{1-r^2} \\ \\ \end{align} \]

where \(k = \left\lceil \frac{90^\circ}{\theta}\right\rceil\) and \(m = \left\lceil \frac{450^\circ}{\theta}\right\rceil\). Then
 

\[ \lim_{r \rightarrow 1^{-}} \frac{r^{m+1} \sin((m-1)\theta) + r^{m+2} \sin(m \theta) - r^{k+1} \sin((k-1)\theta) - r^{k+2}\sin(k\theta)}{1-r^2} = \frac{N(\theta)}{0} = \frac{0}{0}.\\ \\ \]

Therefore we can use L'Hospital's rule to evaluate the limit.

\[ \begin{align} \lim_{r \rightarrow 1^{-}} f_\theta (r) &= \sum_{n=k+1}^{m} \sin(n \theta) \\ \\ &\quad + \frac{(m+1)\sin((m-1)\theta) + (m+2)\sin(m \theta)}{-2} \\ \\ &\quad - \frac{(k+1)\sin((k-1)\theta) + (k+2)\sin(k\theta)}{-2}\\ \\ \end{align} \]

Let's first consider a special case when \(\theta = \frac{540^\circ}{6k} = \frac{90^\circ}{k}\). Then kθ = 90° and 5kθ = 450° so m = 5k. In this case

\[ \begin{align} \sum_{n=k+1}^{m} \sin(n \theta) &= \sum_{n=k+1}^{5k} \sin(n \theta) = \text{Im}\left(\sum_{n=k+1}^{5k} e^{n\theta i}\right) \\ \\ &= \text{Im}\left(\frac{e^{(k+1)\theta i} - e^{(5k+1)\theta i}}{1-e^{\theta i}}\right) \\ \\ &= \text{Im}\left( \frac{e^{k\theta i}e^{\theta i} - e^{5k\theta i}e^{\theta i}}{1-e^{\theta i}}\right) \\ \\ &= \text{Im}\left(\frac{ie^{\theta i} - ie^{\theta i}}{1-e^{\theta i}}\right) = 0 \end{align} \] and \[ \begin{align} &\frac{(m+1)\sin((m-1)\theta) + (m+2)\sin(m \theta) - (k+1)\sin((k-1)\theta) - (k+2)\sin(k\theta)}{-2} \\ \\ &= \frac{(m+1) \cos(\theta) + (m+2) - (k+1) \cos(\theta) - (k+2) }{-2} \\ \\ &= \frac{(5k+1) \cos(\theta) + (5k+2) - (k+1) \sin(\theta) - (k+2) }{-2} \\ \\ &= -2(1+\cos(\theta))k. \\ \\ \end{align} \]

So when \(\theta = \frac{90^\circ}{k}\), then \(\lim_{r \rightarrow 1^{-}} f_\theta (r) = -2(1+\cos(\theta))k\).

What can we say in general? Let \[ \begin{align} g(p) &= \lim_{r \rightarrow 1^{-}} f_\theta (r) = \sum_{n=k+1}^{m} \sin(n \theta) \\ \\ &\quad + \frac{(m+1)\sin((m-1)\theta) + (m+2)\sin(m \theta)}{-2} \\ &\quad - \frac{(k+1)\sin((k-1)\theta) - (k+2)\sin(k\theta)}{-2} \\ \\ \end{align} \] where \(\theta = \frac{540^\circ}{p}\), \(k = \left\lceil\frac{90^\circ}{\theta}\right\rceil \) and \(m = \left\lceil\frac{450^\circ}{\theta}\right\rceil\). Here is the graph of g(p) for p = 4, 5, ..., 40 (black dots). The red dots are at p = 6, 12, 18, 24, and 36, where θ is one of the special cases discussed above. The red graph is \(-2(1+\cos(\theta))k\) for the corresponding theta values for p between 4 and 40.

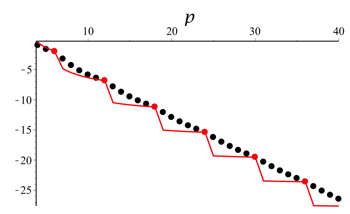
Now let g(p) be the same function but with \(\theta = \frac{360^\circ}{2p+1}\). Here is that graph for p = 1, 2, ..., 13.

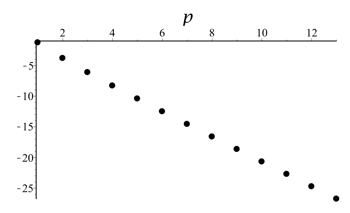
The two graphs together cover all the angles between 13.33333° and 180° that are zeros of N(θ). We see that g(p) is negative for these angles, and the same conclusion would hold for all the zeros.

We have, therefore, that \(\lim_{r \rightarrow 1^{-}} f_\theta (r)\) exists and is negative at each zero of N(θ).