
We will make use of two trig identities: \[ \sin(A) + \sin(B) = 2\sin\left(\frac{A+B}{2}\right)\cos\left(\frac{A-B}{2}\right) \\ \\ \sin(A) - \sin(B) = 2\cos\left(\frac{A+B}{2}\right)\sin\left(\frac{A-B}{2}\right) \]
Using these identities gives \[ \begin{align} N(\theta) &= \left(\sin((m-1)\theta) + \sin(m \theta)\right) -\left(\sin((k-1)\theta) +\sin(k \theta)\right) \\ \\ &= 2\sin\left(\frac{2m-1}{2}\theta\right)\cos\left(\frac{1}{2}\theta\right) - 2\sin\left(\frac{2k-1}{2}\theta\right)\cos\left(\frac{1}{2}\theta\right) \\ \\ &= 2\cos\left(\frac{1}{2}\theta\right) \left[\sin\left(\frac{2m-1}{2}\theta\right) - \sin\left(\frac{2k-1}{2}\theta\right) \right] \\ \\ &= 4\cos\left(\frac{1}{2}\theta\right)\cos\left(\frac{m+k-1}{2}\theta\right)\sin\left(\frac{m-k}{2}\theta\right). \end{align} \]
We first consider \(\theta = \dfrac{540^\circ}{p}\) for integers p in the form p = 6n + b, for n ≥ 0 and b = 0, 1, 2, 3, 4, and 5. (Note that if n = 0, then only b = 3, 4, and 5 give θ ≤ 180°.)
If \(\theta = \dfrac{540^\circ}{6n}\) for n ≥ 1, then \[ \begin{align} k &= \left\lceil{\frac{90^\circ}{\theta}}\right\rceil = \left\lceil{\frac{90(6n)}{540}}\right\rceil = \lceil{n}\rceil = n \\ \\ m &= \left\lceil\frac{450^\circ}{\theta}\right\rceil = \left\lceil\frac{450(6n)}{540}\right\rceil = \left\lceil{5n}\right\rceil = 5n \end{align} \]
Hence \[ \sin\left(\frac{m-k}{2}\theta\right) = \sin\left(\frac{4n}{2}\frac{540^\circ}{6n}\right) = \sin(180^\circ) = 0 \Rightarrow N(\theta) = 0. \] If \(\theta = \dfrac{540^\circ}{6n+b}\) for n ≥ 0, where b = 1, 2, 3, 4, or 5, then \[ \begin{align} k &= \left\lceil{\frac{90^\circ}{\theta}}\right\rceil = \left\lceil{\frac{90(6n+b)}{540}}\right\rceil = \left\lceil{{n+\frac{b}{6}}}\right\rceil = n+1 \\ \\ m &= \left\lceil\frac{450^\circ}{\theta}\right\rceil = \left\lceil\frac{450(6n+b)}{540}\right\rceil = \left\lceil{5n+\frac{5b}{6}}\right\rceil = 5n+b \end{align} \] Hence \[ \cos\left(\frac{m+k-1}{2}\theta\right) = \cos\left(\frac{6n+b}{2}\frac{540^\circ}{6n+b}\right) = \cos(270^\circ) = 0 \Rightarrow N(\theta) = 0. \]Now suppose \(\theta = \dfrac{360^\circ}{2p+1}\). First consider if p = 2n is even. Then \[ \begin{align} k &= \left\lceil{\frac{90^\circ}{\theta}}\right\rceil = \left\lceil{\frac{90(4n+1)}{360}}\right\rceil = \left\lceil{{n+\frac{1}{4}}}\right\rceil = n+1 \\ \\ m &= \left\lceil\frac{450^\circ}{\theta}\right\rceil = \left\lceil\frac{450(4n+1)}{360}\right\rceil = \left\lceil{5n+\frac{5}{4}}\right\rceil = 5n+2 \end{align} \] Hence \[ \sin\left(\frac{m-k}{2}\theta\right) = \sin\left(\frac{4n+1}{2}\frac{360^\circ}{4n+1}\right) = \sin(180^\circ) = 0 \Rightarrow N(\theta) = 0. \] Now if p = 2n+1 is odd, then \[ \begin{align} k &= \left\lceil{\frac{90^\circ}{\theta}}\right\rceil = \left\lceil{\frac{90(4n+3)}{360}}\right\rceil = \left\lceil{{n+\frac{3}{4}}}\right\rceil = n+1 \\ \\ m &= \left\lceil\frac{450^\circ}{\theta}\right\rceil = \left\lceil\frac{450(4n+3)}{360}\right\rceil = \left\lceil{5n+\frac{15}{4}}\right\rceil = 5n+4 \end{align} \] Hence \[ \sin\left(\frac{m-k}{2}\theta\right) = \sin\left(\frac{4n+3}{2}\frac{360^\circ}{4n+3}\right) = \sin(180^\circ) = 0 \Rightarrow N(\theta) = 0. \]
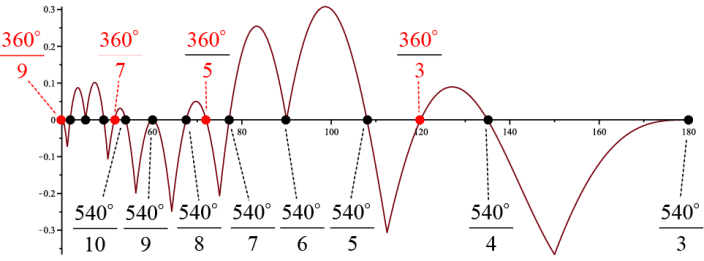
Here is a graph of the zeros for 40° ≤ θ ≤ 180°. Notice that between each pair of red zeros are three black zeros.