


The calculation of the area of the terdragon is based on the construction of the boundary of the terdragon. Let b be the length of the initial line segment in the construction of the terdragon. Then the first iteration for the boundary has the following shape.
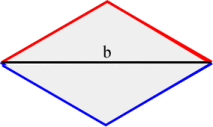
The area of the top triangle is
\[\frac{1}{2} \cdot b \cdot \frac{b}{{2\sqrt 3 }} = \frac{{{b^2}}}{{4\sqrt 3 }}\]and therefore the area of the parallelogram is \(\dfrac{{{b^2}}}{{2\sqrt 3 }}\).
At each iteration of the boundary, the same amount of area is added to the previous region as is removed, as illustrated in the following figures showing the second and third iterations.
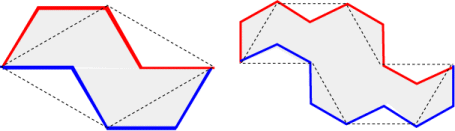
Thus the total area never changes. Since the iterations converge to the boundary of the terdragon, this shows that the area of the terdragon will be \(\dfrac{{{b^2}}}{{2\sqrt 3 }}\).
Another way to calculate the area is to consider the envelopes surrounding each iteration of the terdragon. The figures below show the first four iterations.
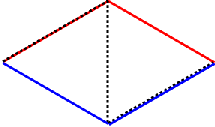
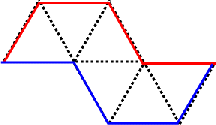
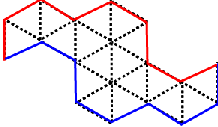
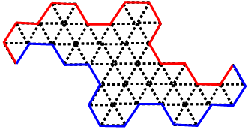
In the top left figure, the area of each triangle is \(\dfrac{{{b^2}}}{{4\sqrt 3 }}\). At each iteration we increase the number of triangles inside the envelope by a factor of 3 while the base of each triangle is scaled by a factor of \(1 / \sqrt 3\). Therefore at the nth iteration, the total area of all the triangles inside the envelope is
\[2 \cdot {3^n} \cdot \frac{{{{\left( {\frac{b}{{{{\left( {\sqrt 3 } \right)}^n}}}} \right)}^2}}}{{4\sqrt 3 }} = \frac{{{b^2}}}{{2\sqrt 3 }}\]The area is the same for all values of n. In the limit the envelopes converge to the boundary of the terdragon, and therefore the area of the terdragon is \(\dfrac{{{b^2}}}{{2\sqrt 3 }}\).