


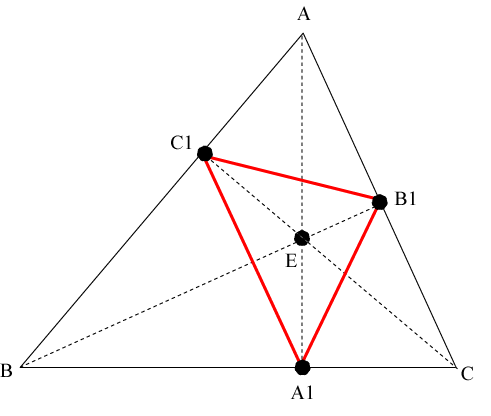
The point E where there three altitudes intersect is the orthocenter of triangle T. The pedal triangle divides the original triangle into four smaller triangles. Remove the interior of the pedal triangle to get S(1).
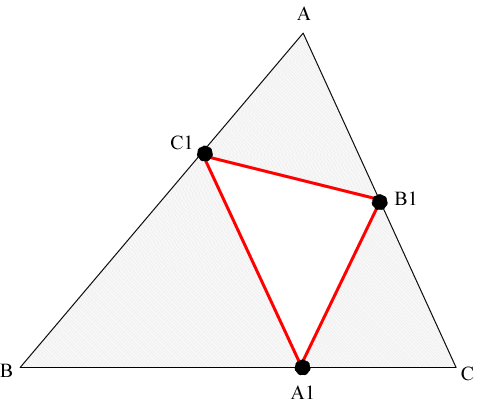
Each of the three remaining triangles is similar to the original triangle T [Proof]. Now repeat this procedure and remove the pedal triangle for each of these three remaining triangles to obtainS(2).
 S(0) |
 S(1) |
 S(2) |
 S(3) |
Continue to repeat the construction to obtain a decreasing sequence of sets
$$ S(0) \supset S(1) \supset S(2) \supset S(3) \supset \cdots $$
The Sierpinski pedal triangle is the intersection of all the sets in this sequence, that is, the set of points that remain after this construction is repeated infinitely often. When the triangle is equilateral, the construction just produces the usual Sierpinski triangle. This generalization of the Sierpinski triangle was first studied in 2008 by Xin-Min Zhang, Richard Hitt, Bin Wang, and Jiu Ding [1].
Construction
Animation

Sierpinski pedal triangle with angles 65°, 50°, and 65°
Try It! Use the slider to change the number of iterations (up to 4). The initial pedal triangle will be highlighted (along with the three triangle altitudes) at the first iteration. You can also click on a vertex and move it with the mouse. Vertices will snap to the grid if close enough. Click the arrows in the upper right to revert back to the initial equilateral position. If the triangle is not acute, no pedal triangles will be drawn. (Note: a lot of calculations are going on behind the scenes each time a vertex is moved, so there will be a slight delay before you see the change.)
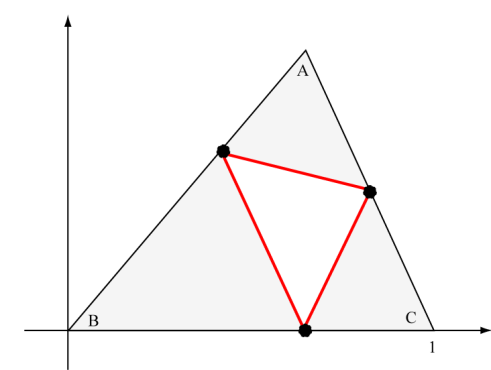
If we let A, B, and C represent the angles in the figure above, then the IFS is given by the following three functions [Proof].
|
\({f_B}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{{{\cos }^2}(B)} & {\cos (B)\sin (B)} \\
{\cos (B)\sin (B)} & { - {{\cos }^2}(B)} \\
\end{array}} \right]{\bf{x}}\) |
scale by cos(B) vertical reflection rotate by B |
|
\({f_C}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{{{\cos }^2}(C)} & { - \cos (C)\sin (C)} \\
{ - \cos (C)\sin (C)} & { - {{\cos }^2}(C)} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{{{\sin }^2}(C)} \\
{\cos (C)\sin (C)} \\
\end{array}} \right]\) |
scale by cos(C) vertical reflection rotate by −C |
|
\({f_A}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ - \cos (A)\cos (C - B)} & {\cos (A)\sin (C - B)} \\
{\cos (A)\sin (C - B)} & {\cos (A)\cos (C - B)} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{{{\sin }^2}(C)} \\
{\cos (C)\sin (C)} \\
\end{array}} \right]\) |
scale by cos(A) horizontal reflection rotate by −(C−B) |
Note: If vertex C is at some other point on the x-axis, then the translation vectors should be multiplied by the length of the segment BC.
The following video shows an animation that summarizes the steps in the iterated function system for generating a Sierpinski pedal triangle.
The Sierpinski Pedal Triangle consists of three self-similar pieces corresponding to the three functions in the iterated function system.
If all three angles are positive, then the derivative of the function \(h(d) = \cos {(A)^d} + \cos {(B)^d} + \cos {(C)^d}\) is \[h'(d) = \ln(\cos A) \cos {(A)^d} + \ln(\cos B)\cos {(B)^d} + \ln(\cos C)\cos {(C)^d}\] which is negative for all \(d >0\) since all the cosine values are less than 1. Since h(0)=3 and \(h\) is strictly decreasing to 0 as d increases, there is a unique solution to \(h(d)=1\). If one of the angles is 90°, say angle \(A\), then the initial triangle is a right triangle and the equation reduces to \(\cos {(B)^d} + \cos {(C)^d} = 1\) where \(B+C = 90^\circ\). Then the unique solution is \(d = 2\) since \[\cos {(B)^2} + \cos {(C)^2} = \cos {(B)^2} + \cos{(90^\circ-B)}^2 = \cos {(B)^2} + \sin {(B)^2} = 1\]
The 65°-50°-65° Sierpinski pedal triangle shown above has dimension 1.59572.
The 70°-60°-60° Sierpinski pedal triangle has dimension 1.60410.
The figures below show a 30°-75°-75° Sierpinski pedal triangle with dimension 1.65931 and a 55°-85°-40° triangle with dimension 1.79750. Ding and Li [2] proved that the ordinary Sierpinski gasket (where all angles equal 60°) has the smallest fractal dimension among all Sierpinski pedal triangles.


Right Triangle
Animation
Transition
Animation