
Let \(\alpha\) be the complex number \(\alpha = e^{\theta i}=\cos{\theta} + i \sin{\theta}\). We can represent the trunk of the tree by the complex number \(i\) (which we can also think of geometrically as a vector). Recall that multiplying a vector by r will scale the vector by r, that multiplying the vector by \(\alpha\) corresponds to a counterclockwise rotation by θ, and multiplying by \(\alpha^{-1}\) corresponds to a clockwise rotation by θ. We also have \(\alpha^n = e^{n\theta i}=\cos{(n\theta)} + i \sin{(n\theta)}\) and \(\alpha^{-n} = e^{-n\theta i}=\cos{(n\theta)} - i \sin{(n\theta)}\) for all integers n.
For this path we thus have \(x = \text{Re}(iz) = -\text{Im}(z) = \dfrac{-r \,\sin{(\theta)}}{1-r^2}\) and \(y = \text{Im}(iz) = \text{Re}(z) = \dfrac{1+r\, \cos{(\theta)}}{1-r^2}\).
R6(LR)4, θ=70°
The branch tip for Rk(LR)∞ corresponds to the complex number
\( \left(i + i r \alpha^{-1} + i r^2 \alpha^{-2} + \ldots + i r^k \alpha^{-k}\right) + i r^k \alpha^{-k} \cdot \left( {r \alpha + r^2 + r^3 \alpha + r^4 + \dots} \right) \) \[ \begin{align} &= i \left( \sum_{n=0}^{k}{r^n \alpha^{-n}} + r^k \alpha^{-k} \cdot \left( \dfrac{ra}{1-r^2} + \frac{r^2}{1-r^2} \right) \right) \\ \\ &= i \left( \sum_{n=0}^{k}{r^n \alpha^{-n}} + \frac{r^{k+1}\alpha^{-(k-1)} + r^{k+2}\alpha^{-k}}{1-r^2} \right) = iz. \end{align} \]The y-coordinate of this branch tip is \(\text{Im}(iz) = \text{Re}(z)\), or
\[ \sum_{n=0}^{k}{r^n \cos(n \theta)} + \frac{r^{k+1} \cos((k-1)\theta) + r^{k+2} \cos(k \theta)}{1-r^2}. \]
θ = 150°, r = 0.8
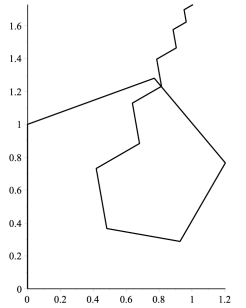
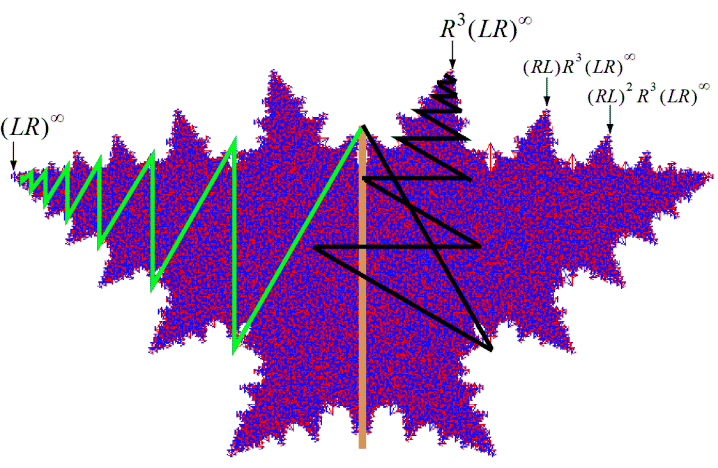
The black path for R3(LR)∞ has a branch tip with y-coordinate 1.19607 while the green path for (LR)∞ leads to a branch tip with y-coordinate only at 0.85328 (the x-coordinates are 0.28262 and −1.11111, respectively). You can get a sense of why this might happen in this example since the green path has mostly a horizontal direction while the black path is more vertical. The value of r is large enough that the black path will grow sufficiently upward to eventually extend above the end of the green path. You can see this happen by viewing the branch animation. If you watch the tree animation, you will see how this large value of r produces extensive overlap of the branches as the tree grows. Also notice in the figure above that the other "peaks" along the boundary are extensions of R3(LR)∞ using initial branches of the form (RL)m.
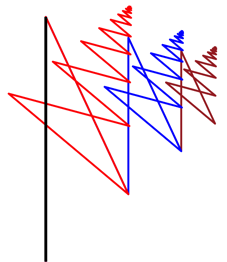
θ = 150°, r = 0.8
red: R3(LR)∞
blue: (RL)R3(LR)∞
brown: (RL)2R3(LR)∞
For this special case we have kθ = 360° and therefore the last branch of Rk is vertical, but of length rk. From this point on, the branches of Rk(LR)∞ alternate in the same pattern that the (LR)∞ branches did from the beginning, but can never catch up, and thus yk will be less than y0. The following image shows what happens for θ = 120° with r = 0.9. The red path will have y0 = 2.89474 and the black path will have y3 = 2.25526.
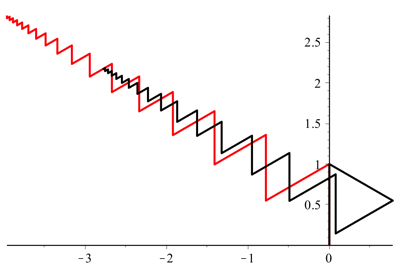
θ = 120°, r = 0.9
Why does this happen for these special values of θ? Because kθ = 360°, \(\cos(k \theta) = \cos(360^{\circ}) = 1\) and \(\cos((k-1)\theta) = \cos(360^{\circ}-\theta) = \cos(\theta)\). Therefore
\[ f_\theta (r) = \sum_{n=0}^{k}{r^n \cos(n \theta)} + \frac{r^{k+1} \cos(\theta) + r^{k+2} -1-r\cos( \theta)}{1-r^2}. \]It can then be shown [Details] that the graph of \(f_\theta (r)\) starts at (0,0) and initially begins decreasing in a concave down fashion as r increases. Moreover, with the help of L'Hospital's rule, we can determine that
\[ \begin{align} \lim_{r \rightarrow 1^{-}} f_\theta(r) &= \sum_{n=0}^{k}{\cos(n \theta)} + \lim_{r \rightarrow 1^{-}} \frac{(k+1)r^k \cos(\theta) + (k+2)r^{k+1} - \cos(\theta)}{-2r} \\ \\ &= 1 + \frac{(k+1)\cos(\theta)+k+2-\cos(\theta)}{-2} = -\frac{k}{2}(1+\cos(\theta)). \end{align} \]Therefore \(\lim_{r \rightarrow 1^{-}} f_\theta(r) < 0\) suggesting that \(f_\theta(r)\) always remains negative as r goes from 0 to 1. This would imply that y0 is always greater than yk for all r between 0 and 1 for these special values of θ. To see that this is actually the case, click on the Play button below to see the graphs of \(f_\theta(r)\) for k from 3 to 360, corresponding to the 358 special θ values of the form 360°/k between 1° and 120°. The graph is shown only for 0.9 ≤ r ≤ 1 since the scale on the vertical axis will prevent the very small values of \(f_\theta(r)\) from being shown for small values of r.
Now the smallest integer k such that kθ > 360° is \(k = \left\lceil \frac{360^\circ}{\theta} \right\rceil\), where \(\lceil x \rceil\) is the ceiling function, i.e. the smallest integer greater than or equal to x. As in case 1, the value of k can be any integer greater than or equal to 3.
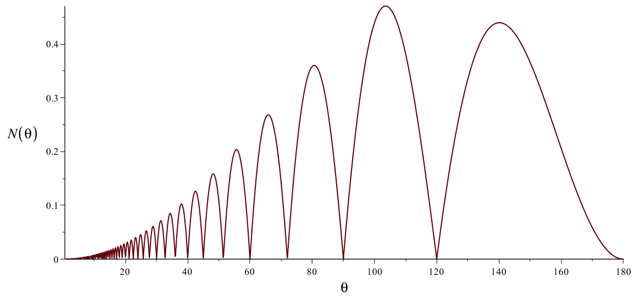
As before [Details], the graph of \(f_\theta (r)\) starts at (0,0) and initially begins decreasing in a concave down fashion as r increases. This time, however, we have \(\lim_{r \rightarrow 1^{-}} f_\theta (r) = +\infty\). To see why, we just need to verify that the numerator of the fraction in the expression for \(f_\theta (r)\) is positive when r = 1 since the denominator is positive and goes to 0 as r approaches 1 from the left. So we need to verify that \[ N(\theta) = \cos((k-1)\theta) + \cos(k \theta) -1-\cos( \theta) > 0 \text{ when } \frac{360^\circ}{k} < \theta < \frac{360^\circ}{k-1} \] where \(k = \lceil \frac{360^\circ}{\theta} \rceil\). For example, for 120° < θ < 180° with k = 3, \[N(\theta) = \cos(2\theta) + \cos(3 \theta) -1-\cos( \theta) = -2 \sin^2(\theta) (2\cos(\theta)+1) > 0\] since \(2\cos(\theta)+1 < 0\) for 120° < θ < 180°. Note that N(120°) = N(180°) = 0, and that in general, N(360°/k) = N(360°/(k-1)) = 0.
Shown below is the graph of \(N(\theta)\) showing that \(N(\theta)\) is positive for all θ except for those of the form 360°/k (which pile up very quickly as k gets large and θ approaches 0.)
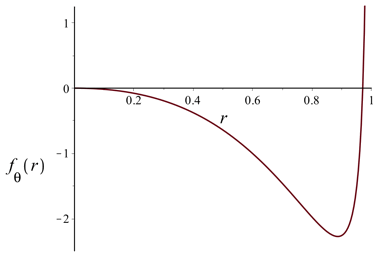
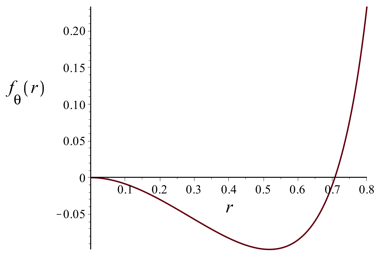
Because \(f_\theta (r)\) is negative for small r and \(\lim_{r \rightarrow 1^{-}} f_\theta (r) = +\infty\), there must be some some rT between 0 and 1 where \(f_\theta (r_T) = 0.\) The two images below show the graphs of \(f_\theta (r)\) for θ = 65° and θ = 135°. The shapes of these graphs are typical for all values of θ in case 2.
|
|
|
| θ = 65° rT = 0.96984 |
θ = 135° rT = \(\frac{1}{\sqrt{2}}\) = 0.70711 |
The equation \(f_\theta (r) = 0\) can be solved numerically to find the solution rT. The next two figures show the graph of rT for 0° < θ < 180°, and a close up of this graph just on the range 10° < θ < 90°.
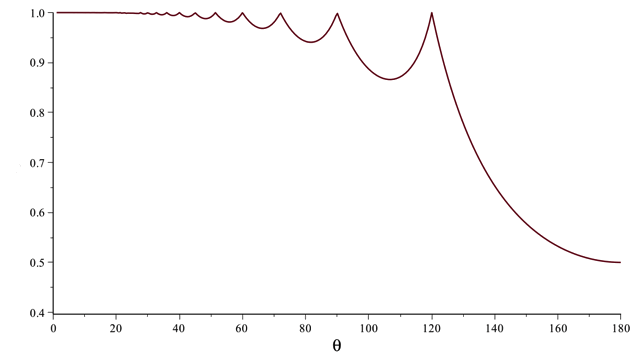
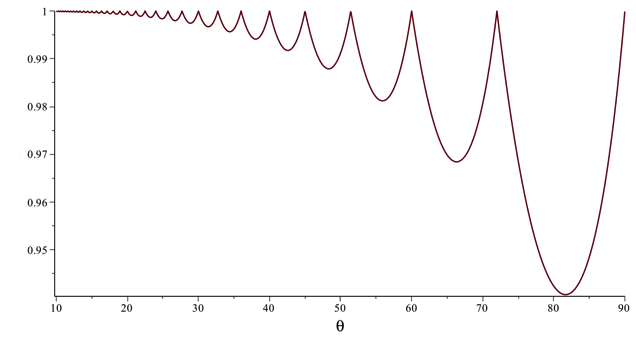
Several observations. First, the equation \(f_\theta (r) = 0\) has no solution for r > 0 when θ is of the form 360°/k for some integer k. These are the special angles in case 1. Therefore rT does not exist at these special values of θ. However, what the graphs show is that rT approaches 1 as θ approaches one of these special angles.
Second, for θ < 90°, the value of the critical scaling factor rT is greater than 0.94, so for all practical purposes the top of a "reasonable" symmetric binary tree for this range of θ will be determined by the (LR)∞ path and have value \((1+r\cos(\theta))/(1-r^2)\). Any choice of r > 0.94 will produce a tree that has a massive overlap of branches.
Third, the situation is a bit different for θ > 90°, and in particular for θ > 120°. Note that on this latter interval, the value of rT converges to 1/2 as θ approaches 180°. We can, in fact, solve \(f_\theta (r) = 0\) explicitly for r for those values of θ in these two intervals [Calculation Details] to get \[ \begin{align} 90^\circ < \theta < 120^\circ &\Rightarrow r_T = - \frac{{\cos ( {{{\theta}}} ) + \sqrt { - 3\cos^2 {{( {{{\theta}}} )}} + 1} }}{{4\cos^2 {{( {{{\theta}}} )}} - 1}} \\ \\ 120^\circ < \theta < 180^\circ &\Rightarrow r_T = -\frac{1}{2\cos(\theta)} \end{align} \]
Finally, it is interesting to note that for θ ≥ 135°, the critical scaling factor rT is the same value as rsc for which the binary tree of angle θ is self-contacting. Here is a comparison of the two graphs of rT versus rsc. For rsc < r < rT, the binary tree will have overlapping branches, but the top of the branch tips will still correspond to the (LR)∞ path.
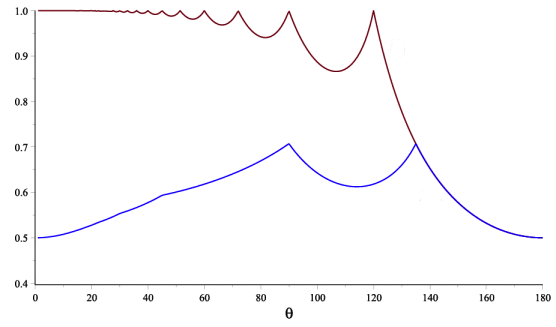
brown: rT
blue: rsc